Malaria disease overview¶
IDM is committed to supporting data-driven malaria control and elimination efforts. This page provide information about malaria itself: the biology, symptoms, treatment, and prevention. See Malaria model for information about the Epidemiological MODeling software (EMOD) MALARIA simulation type developed by IDM to aid in malaria elimination.
Malaria biology¶
Malaria is a mosquito-borne disease caused by plasmodium parasites transmitted through the bite of blood-feeding Anopheles mosquitos. There are roughly 30 species of Anophelenes capable of serving as malaria vectors, and only females bite (i.e. seek blood meals) to gain nutrients necessary for oviposition. After taking blood meals, females lay eggs in water sources, where the emerging larvae hatch and mature. Each species of Anopheles has different aquatic habitat preferences, ranging from small, ephemeral pools to large swampy areas, and in some cases, brackish water.
Transmission of malaria depends on both biotic and abiotic factors. Mosquito lifespan is positively correlated to transmission intensity. Mosquito populations, and therefore transmission, tend to be seasonal with dependence on climatic conditions such as rainfall patterns, humidity, and temperature. Typically, malaria transmission peaks during and after the rainy season, when conditions are prime for mosquito reproduction. Additionally, transmission is dependent on human immunity: people living in areas of high exposure to malaria can develop partial immunity, which reduces the risk of developing severe disease. Unfortunately, such partial immunity may mask symptoms of disease (and obscure infection), which may hinder control or elimination efforts.
Once an infected mosquito bites a human and transmits parasites, the parasites multiply in the host’s liver, then infect and destroy red blood cells (erythrocytes). During the blood stage, the parasites that infect and destroy erythrocytes release merozoites which then infect other erythrocytes. The gametocyte form of the blood-stage parasite are ingested by female Anophelenes during future blood meals, where the mosquito-based life cycle continues.
In the mosquito, the ingested gametocytes generate zygotes in the mosquito’s gut. Those zygotes undergo development, embed into the mosquito’s midgut wall, and mature into oocytes. Oocytes develop and in turn rupture, releasing the sporozoite form of the parasite. The sporozoites travel to and reside in the mosquito’s salivary glands. Then, when the female takes a blood meal, the sporozoites are injected into the host, starting another infection cycle. The mosquito is the vector that transmits pathogens between human hosts. See the below figure and figure caption for an illustrated description of this process.

Plasmodium life cycle, adapted from the CDC, Malaria Biology. During a blood meal, a malaria-infected female Anopheles mosquito inoculates sporozoites into the human host (1) . Sporozoites infect liver cells (2) and mature into schizonts (3), which rupture and release merozoites (4). After this initial replication in the liver (exo-erythrocytic schizogony, “A”), the parasites undergo asexual multiplication in the erythrocytes (erythrocytic schizogony, “B”). Merozoites infect red blood cells (5). Some parasites differentiate into sexual erythrocytic stages (gametocytes) (7). The gametocytes are ingested by an Anopheles mosquito during a blood meal (8). The parasites’ multiplication in the mosquito is known as the sporogonic cycle, “C”. While in the mosquito’s stomach, the gametocytes generate zygotes (9). The zygotes in turn become motile and elongated (ookinetes) (10) which invade the midgut wall of the mosquito where they develop into oocysts (11). The oocysts grow, rupture, and release sporozoites (12), which make their way to the mosquito’s salivary glands. Inoculation of the sporozoites into a new human host (1) perpetuates the malaria life cycle.¶
Symptoms¶
All the clinical symptoms associated with malaria are caused by the asexual erythrocytic (or blood stage) parasites. Malaria has a long incubation period, so symptoms do not develop immediately after a person has been bitten by an infectious mosquito; they can occur 7 days after infection, but this may vary up to 30 days.
Symptoms of malaria range in severity, but include fever, headache, body-ache, chills, and vomiting. Severe malaria can develop when the infection is not treated, and may result in organ failure or even death. Examples of severe malaria include cerebral malaria, severe anemia, respiratory distress (due to accumulated fluid in the lungs), kidney failure, metabolic acidosis, hypoglycemia, and other maladies. Death can occur from anemia, hypoglycemia, or cerebral malaria (where capillaries leading to the brain are blocked; typically resulting in coma, brain damage or learning disabilities).
Confirmed diagnosis of malaria is done through observation of parasites in the blood, as seen on the below microscopic image. In highly endemic areas, treatment typically occurs prior to diagnostic confirmation, as malaria is more easily cured with prompt treatment.
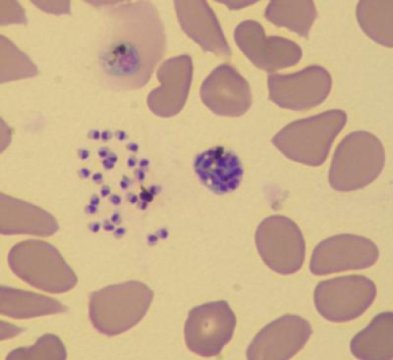
Human red blood cells infected with Plasmodium falciparum (the parasite is shown in dark purple). Photo credit Le Roch lab, UC Riverside.¶
Prevention & control efforts¶
There are numerous types of strategies used to control malaria. As a vector-borne disease, there are multiple stages at which the transmission cycle can be broken.
Vector control: strategies that take into account vector ecology. These include:
Chemical control, such as insecticide spraying or use of larvicides.
Reduction of or elimination of mosquito larval habitat, through drainage or use of biological controls.
Potential use of genetic modification (with tools such as CRISPR) to create mosquitoes that are resistant to infection from Plasmodium parasites.
Potential use of the bacterium Wolbachia to prevent mosquitoes from becoming infectious.
Personal protection: strategies that avoid infection (by avoiding bites by infectious mosquitoes), or by preventing disease. These include:
The use of insecticide-treated nets (ITN)
Administration of antimalarial drugs to particularly vulnerable groups, such as children or pregnant women
Global malaria burden¶
While progress towards reducing the malaria burden has been largely successful, malaria nevertheless remains a major health problem and target of focused, global efforts for elimination and eradication. According to the CDC, 3.2 billion people worldwide are at risk of malaria. In 2015, there were 214 million cases with 483,000 deaths. Malaria is especially harmful to children: more than 70% of all malaria deaths occur in children under the age of 5. To put that in perspective, a child dies from malaria roughly every 2 minutes.
While malaria is a global problem, the burden is not distributed equally across the globe. Sub-Saharan Africa experiences a disproportionately high burden, with about 76% of all cases and 75% of all deaths. South East Asia, Latin America, and the Middle East are also at high risk for malaria.
Benefits of mathematical models in malaria control and eradication¶
Control and eventual eradication of malaria will require multifaceted and geographically-specific intervention efforts. Heterogeneity in transmission, and transmission potential, creates a need for combinations of interventions that can adapt to the particular malaria epidemiology of the target area.
For malaria, mathematical modeling and simulations are key to achieving eradication. Species- specific vector ecology is a fundamental driver of transmission, and transmission is also impacted by the interactions of climate, human behavior, and land usage, across varying spatial scales. Modeling these factors enables accurate representations of baseline transmission, which in turn provides a platform to test various interventions (such as insecticide-treated nets (ITN), indoor residual spraying (IRS), or mass drug administration (MDA)) and combinations of interventions. These simulation results can inform policy to develop effective–and cost effective–strategies by exploring the many possible dimensions of coverage, frequency of distribution, and combinations of interventions targeted to particular locations.
It should be noted that such a multifaceted and integrated approach to vector control and health management is the most likely path towards elimination, as heavy reliance on singular approaches can be problematic. For example, vector control has been widely implemented and quite successful; however, mosquitoes are developing resistance to pyrethroids, one of the most common classes of insecticides currently recommended for ITN or IRS to control mosquito populations. Through modeling approaches, researchers will be able to develop strategies that lessen dependence on particular insecticides while maintaining successful control efforts.
A brief history of malaria modeling¶
Malaria has a long history of posing risks to public health, and as such, also has long been the target of mathematical models tasked with providing solutions to ease the burden. For a more detailed history of malaria models, see Smith et al. PLOS Pathogens 2012 8(4), and Smith et al. Trans R Soc Trop Med Hyg 2014 108(4). The EMOD malaria model builds upon this rich history of disease modeling to provide a novel and rigorous approach to help guide efforts towards malaria elimination and eradication. To fully understand the strengths of EMOD, it is helpful to understand the modeling background from which EMOD developed.
Arguably, the quantitative analysis of mosquito-borne diseases, specifically malaria, began with Ronald Ross. In 1897 Ross confirmed that mosquitoes serve as the vector for malaria parasites, and embarked on a career focused on disease prevention through vector control. Further, Ross developed the modeling framework that serves as the basis for studying malaria transmission dynamics.
Ross’s work inspired researchers focused on controlling mosquito-borne diseases. His emphasis on the development of metrics useful for measuring the intensity of transmission led to the development of :term:` entomological inoculation rate (EIR)` and motivated research aimed at understanding mosquito movement and the relevant spatial scales for mosquito ecology. Later, in the 1950s, George MacDonald formalized Ross’s models, and introduced the concepts of vectorial capacity and reproductive number. This framework is now known as the Ross-Macdonald model, and is still widely implemented in current modeling work. In fact, the vast majority of models created in the last 40 years share most of their assumptions with the Ross-Macdonald model (see Reiner et al. 2013, Journal of the Royal Society Interface.)
The Garki project¶
The Garki project was a major milestone in malaria research. From 1969 to 1976 this study was conducted by the World Health Organization (WHO) and the local government of the Jigawa State, Nigeria, to understand the impacts of indoor residual spraying (IRS) and mass drug administration (MDA) on malaria transmission, as well as to evaluate the utility of mathematical modeling. While the interventions used did not interrupt transmission at the desired level, the model proved to be a success. The epidemiology of the Plasmodium parasite was realistically replicated, even with a simplistic model, and as a result understanding of the parasite’s epidemiology was greatly increased.
While the project was largely considered a failure in terms of malaria control, much was gained from the project. Basic tenets of malaria control were learned– namely, that malaria ecology needs to be fundamentally altered: either by modification of mosquito ecology, or by changing human ecology such as by improving housing conditions. A superinfection, a fundamental malaria concept modeled by Macdonald in his first malaria model publication [Macdonald-1950], was more correctly described by Dietz [Dietz-1974]. Further, the data set from the project is publicly available, and has become a fundamental tool for use in malaria modeling. For more information on this project, see The Garki Project.
Moving forward¶
The Ross-Macdonald model, while extremely useful and influential, has some shortcomings. The model assumes homogeneous transmission within a well-mixed population. Host-vector ratios and numerous aspects of mosquito feeding and development biology is assumed to remain constant. Further, all hosts are assumed to be identical, with equal exposure to pathogens, and the probability of transmission is proportional to host and vector densities. Interestingly, despite work demonstrating that these assumptions are not realistic, many models still utilize them.
To improve on the Ross-Macdonald model, it is necessary to understand and implement increased complexity into the transmission dynamics of the model. Transmission dynamics are not linear, and instead depend on fine-scale heterogeneities; ecological as well as social contexts are extremely relevant for potential host-vector interactions, and both human and mosquito movement across relevant spatial scales also impact malaria transmission.
Modern research has continued to improve our understanding of both parasite biology (and genetics) as well as within-host immune system interactions. To fully understand the complex nature of malaria epidemiology and how to control it, it is important to include these aspects into models.
The malaria EMOD leverages the history of malaria modeling by staring with these important fundamentals and building upon them. EMOD combines detailed vector population dynamics and interactions with human populations, and includes microsimulations for human immunity and within- host parasite dynamics. The model builds on the work of Ross and MacDonald, leverages the Garki model, and incorporates current modeling efforts to model multiple vector species simultaneously interacting with a human population.
References¶
Macdonald G (1950) The analysis of infection rates in diseases in which superinfection occurs. Trop Dis Bull 47: 907–915.
Dietz K, Molineaux L, Thomas A (1974) A malaria model tested in the African savannah. Bull World Health Organ 50: 347–357