SEIR and SEIRS models¶
This topic describes the differential equations that govern the classic deterministic SEIR and SEIRS compartmental models and describes how to configure EMOD, an agent-based stochastic model, to simulate an SEIR/SEIRS epidemic. In this category of models, individuals experience a long incubation duration (the “exposed” category), such that the individual is infected but not yet infectious. For example chicken pox, and even vector-borne diseases such as dengue hemorrhagic fever have a long incubation duration where the individual cannot yet transmit the pathogen to others.
The SEIR/SEIRS diagram below diagram below shows how individuals move through each compartment in the model. The dashed line shows how the SEIR model becomes an SEIRS (Susceptible - Exposed - Infectious - Recovered - Susceptible) model, where recovered people may become susceptible again (recovery does not confer lifelong immunity). For example, rotovirus and malaria are diseases with long incubation durations, and where infection only confers temporary immunity.
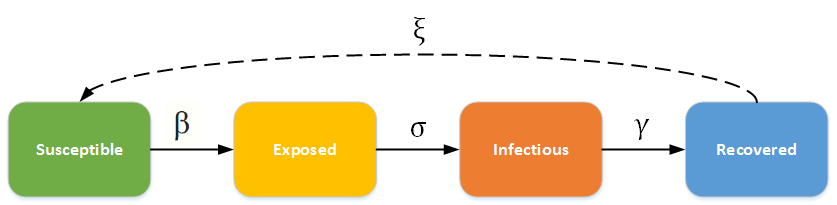
SEIR - SEIRS model¶
The infectious rate, \(\beta\), controls the rate of spread which represents the probability of transmitting disease between a susceptible and an infectious individual. The incubation rate, \(\sigma\), is the rate of latent individuals becoming infectious (average duration of incubation is 1/\(\sigma\)). Recovery rate, \(\gamma\) = 1/D, is determined by the average duration, D, of infection. For the SEIRS model, \(\xi\) is the rate which recovered individuals return to the susceptible statue due to loss of immunity.
Contents
SEIR model¶
Many diseases have a latent phase during which the individual is infected but not yet infectious. This delay between the acquisition of infection and the infectious state can be incorporated within the SIR model by adding a latent/exposed population, E, and letting infected (but not yet infectious) individuals move from S to E and from E to I. For more information, see Incubation parameters.
SEIR without vital dynamics¶
In a closed population with no births or deaths, the SEIR model becomes:
where \(N = S + E + I + R\) is the total population.
Since the latency delays the start of the individual’s infectious period, the secondary spread from an infected individual will occur at a later time compared with an SIR model, which has no latency. Therefore, including a longer latency period will result in slower initial growth of the outbreak. However, since the model does not include mortality, the basic reproductive number, R0 = \(\beta/\gamma\), does not change.
The complete course of outbreak is observed. After the initial fast growth, the epidemic depletes the susceptible population. Eventually the virus cannot find enough new susceptible people and dies out. Introducing the incubation period does not change the cumulative number of infected individuals.
The following graphs show the inset chart and charts for all channels in a couple typical SEIR outbreaks, one with an incubation period of 8 days and one with an incubation period of 2 days. Notice how the outbreak depletes the susceptible population more quickly when the incubation period is shorter but that the cumulative infections remains the same. To run this example simulation, see the Generic/SEIR scenario in the downloadable EMODScenarios folder. Review the README files there for more information.
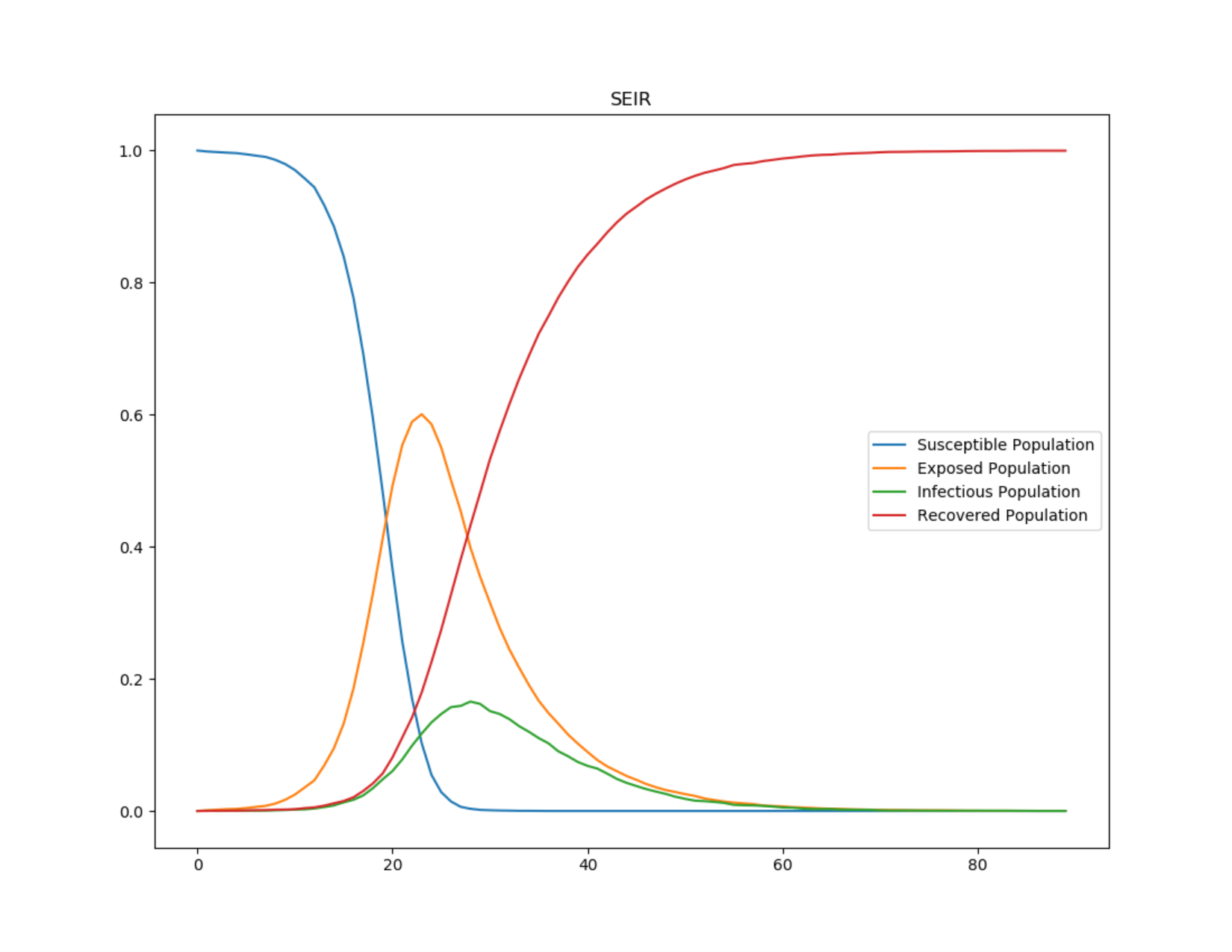
Figure 1: SEIR epidemic course for 8-day incubation period¶
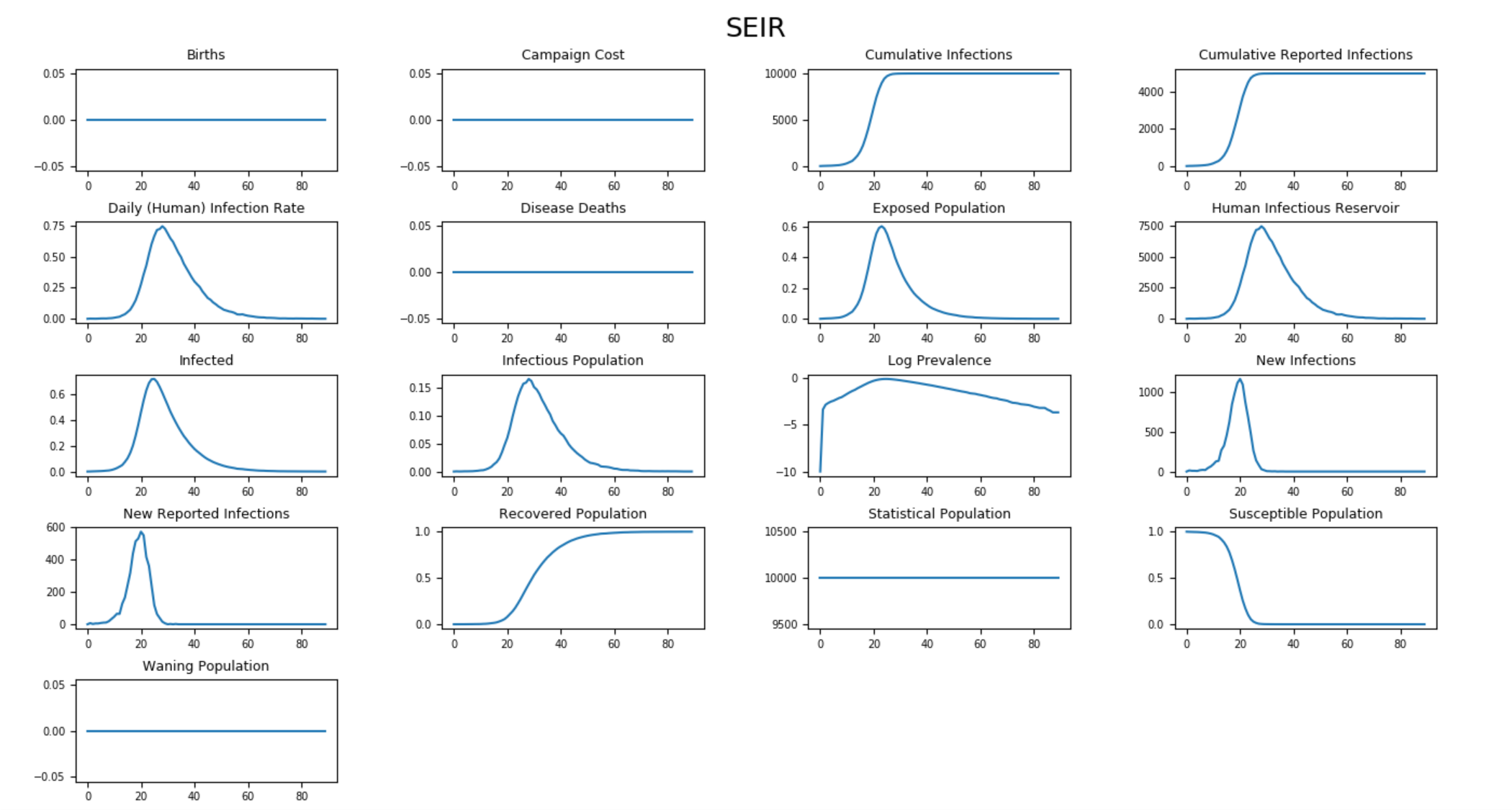
Figure 2: All output channels for SEIR 8-day incubation period¶
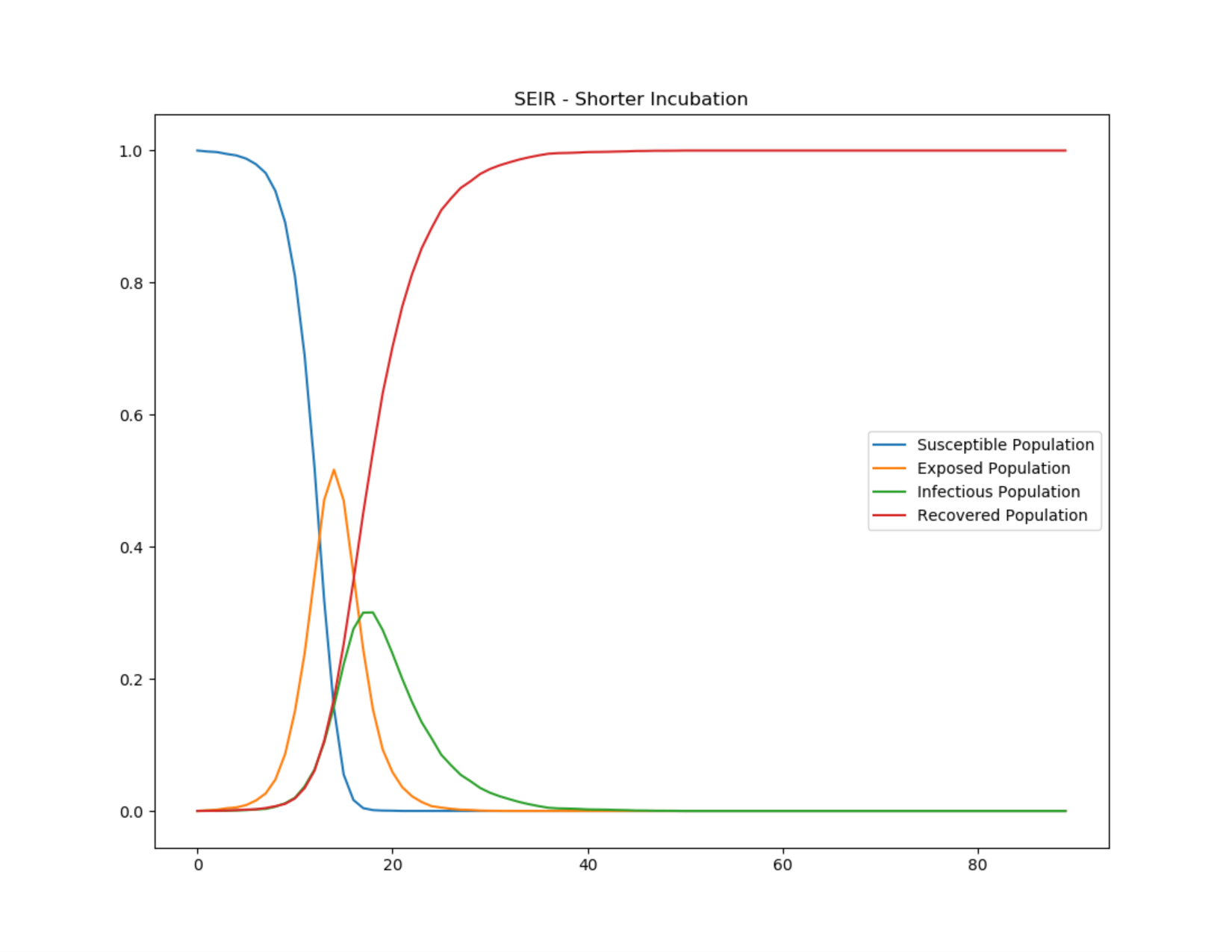
Figure 3: SEIR epidemic course for 2-day incubation period¶
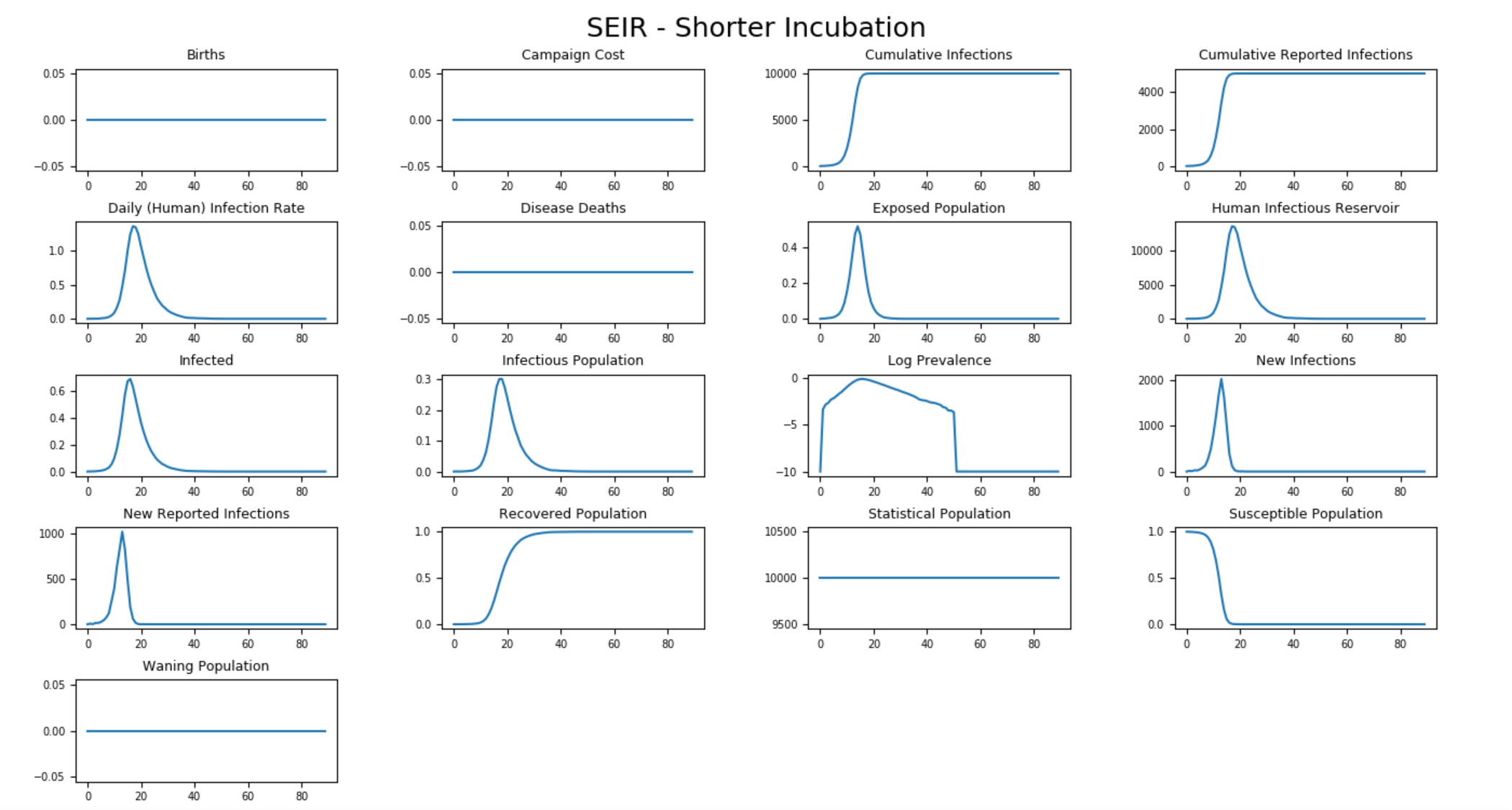
Figure 4: All output channels for SEIR 2-day incubation period¶
SEIR with vital dynamics¶
As with the SIR model, enabling vital dynamics (births and deaths) can sustain an epidemic or allow new introductions to spread because new births provide more susceptible individuals. In a realistic population like this, disease dynamics will reach a steady state. Where \(\mu\) and \(\nu\) represent the birth and death rates, respectively, and are assumed to be equal to maintain a constant population, the ODE then becomes:
where \(N = S + E + I + R\) is the total population.
The following graphs show periodic reintroductions of an SEIR outbreak in a population with vital dynamics. To run this example simulation, see the Generic/SEIR_VitalDynamics scenario in the EMODScenarios folder. Review the README files there for more information.
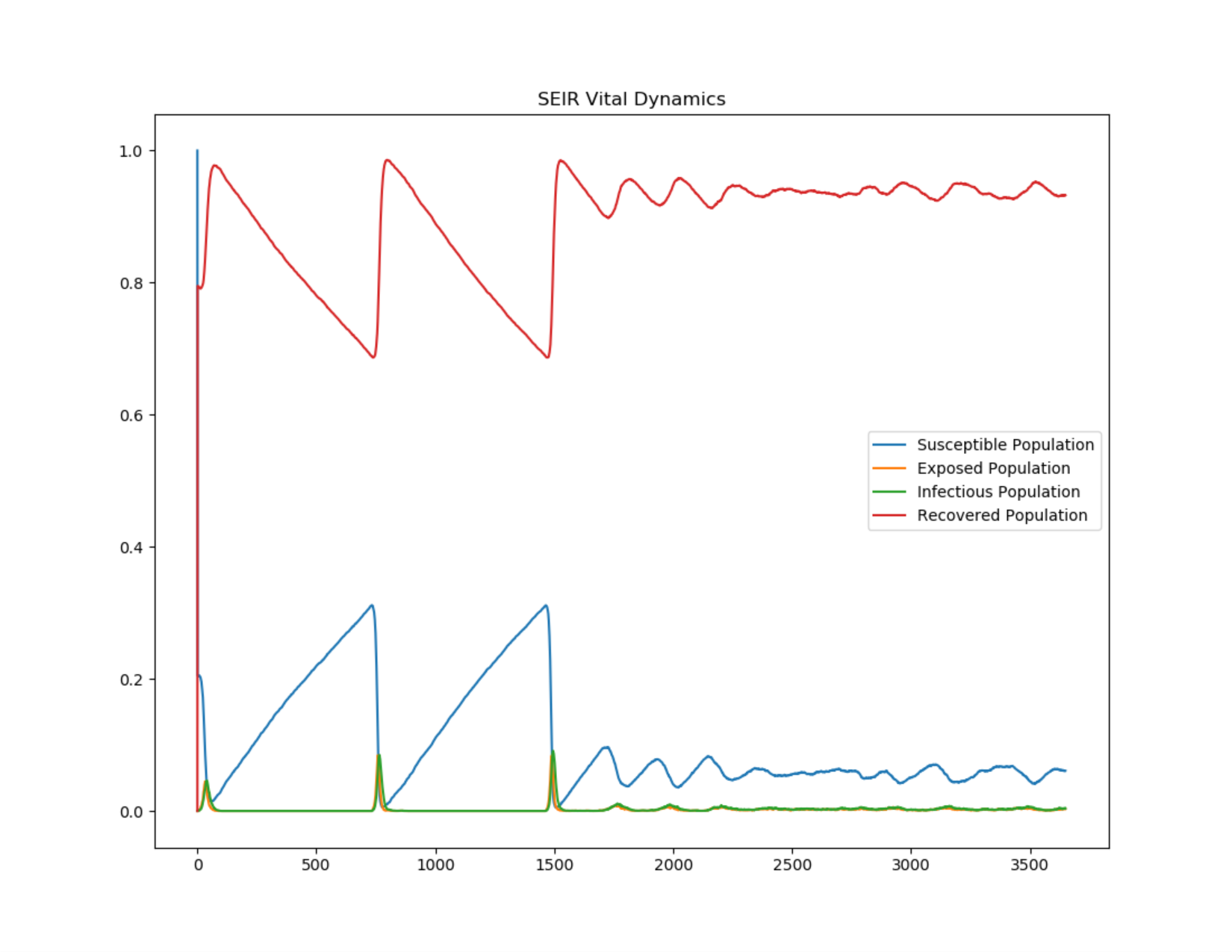
Figure 5: SEIR periodic outbreaks on reintroduction in a population with vital dynamics¶
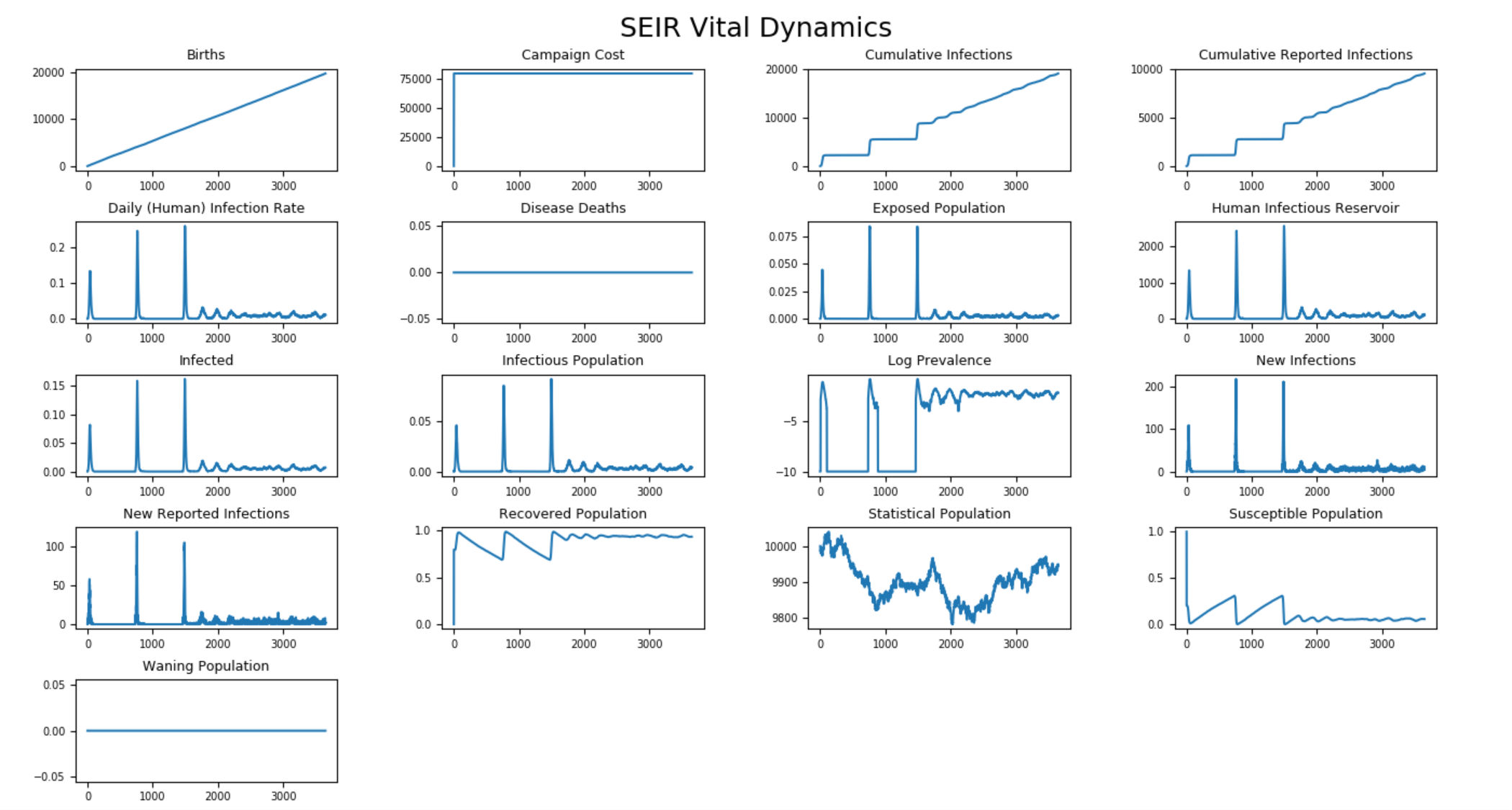
Figure 6: All output channels for SEIR outbreaks¶
SEIRS model¶
The SEIR model assumes people carry lifelong immunity to a disease upon recovery, but for many diseases the immunity after infection wanes over time. In this case, the SEIRS model is used allow recovered individuals return to a susceptible state. Specifically, \(\xi\) is the rate which recovered individuals return to the susceptible statue due to loss of immunity. If there is sufficient influx to the susceptible population, at equilibrium the dynamics will be in an endemic state with damped oscillation. The SEIRS ODE is:
where \(N = S + E + I + R\) is the total population.
EMOD simulates waning immunity by a delayed exponential distribution. Individuals stay immune for a certain period of time then immunity wanes following an exponential distribution. For more information, see Immunity parameters.
SEIRS with vital dynamics¶
You can also add vital dynamics to an SEIRS model, where \(\mu\) and \(\nu\) again represent the birth and death rates, respectively. To maintain a constant population, assume that \(\mu = \nu\). In steady state \(\frac{dI}{dt} = 0\). The ODE then becomes:
where \(N = S + E + I + R\) is the total population.
The following graphs show the complete trajectory of a fatal SEIRS outbreak: the disease endemicity due to vital process and waning immunity and the effect of vaccination campaigns that eradicate the outbreak after day 500. To run this example simulation, see the Generic/SEIRS scenario in the downloadable EMODScenarios folder. Review the README files there for more information. For more information on creating campaigns, see Creating campaigns.
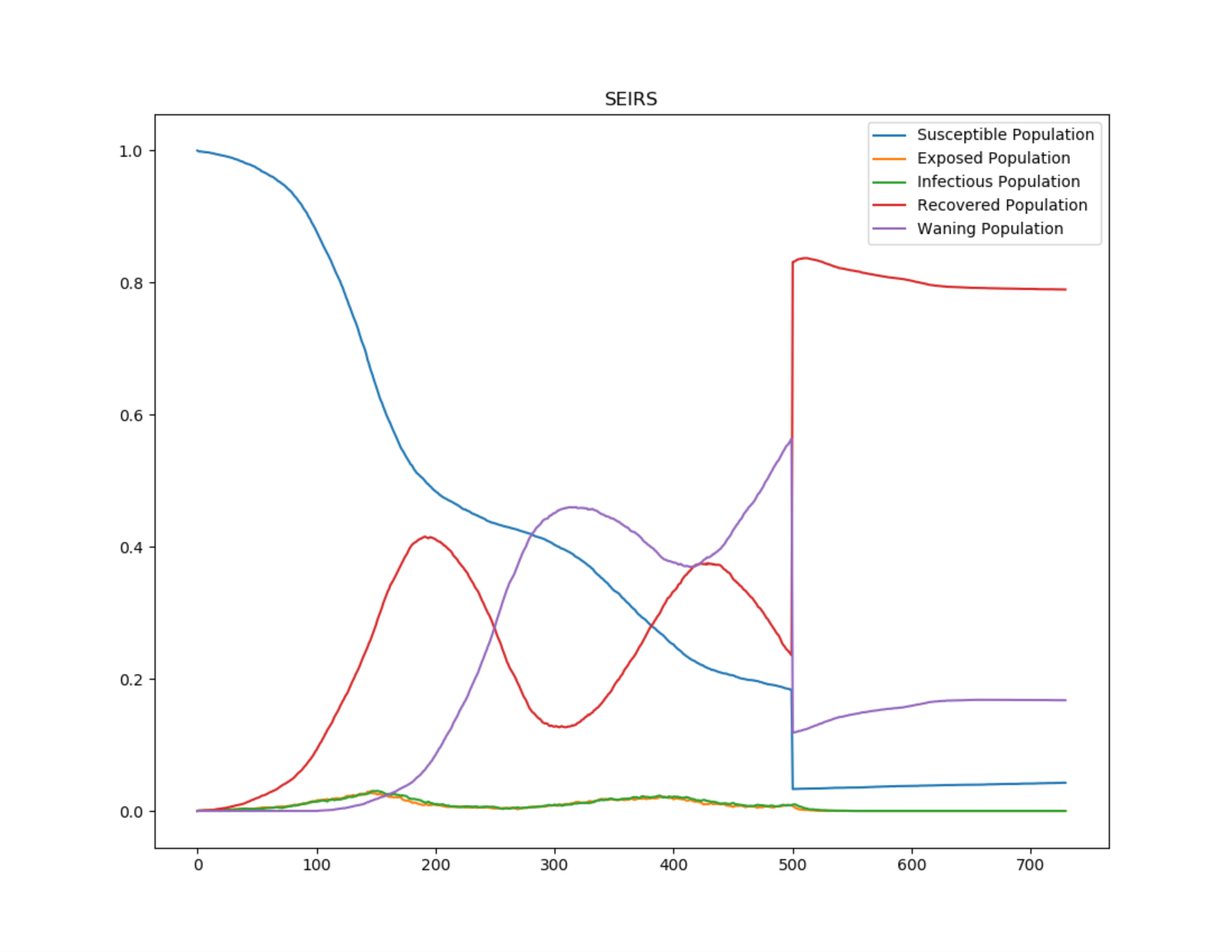
Figure 7: Trajectory of the SEIRS outbreak¶
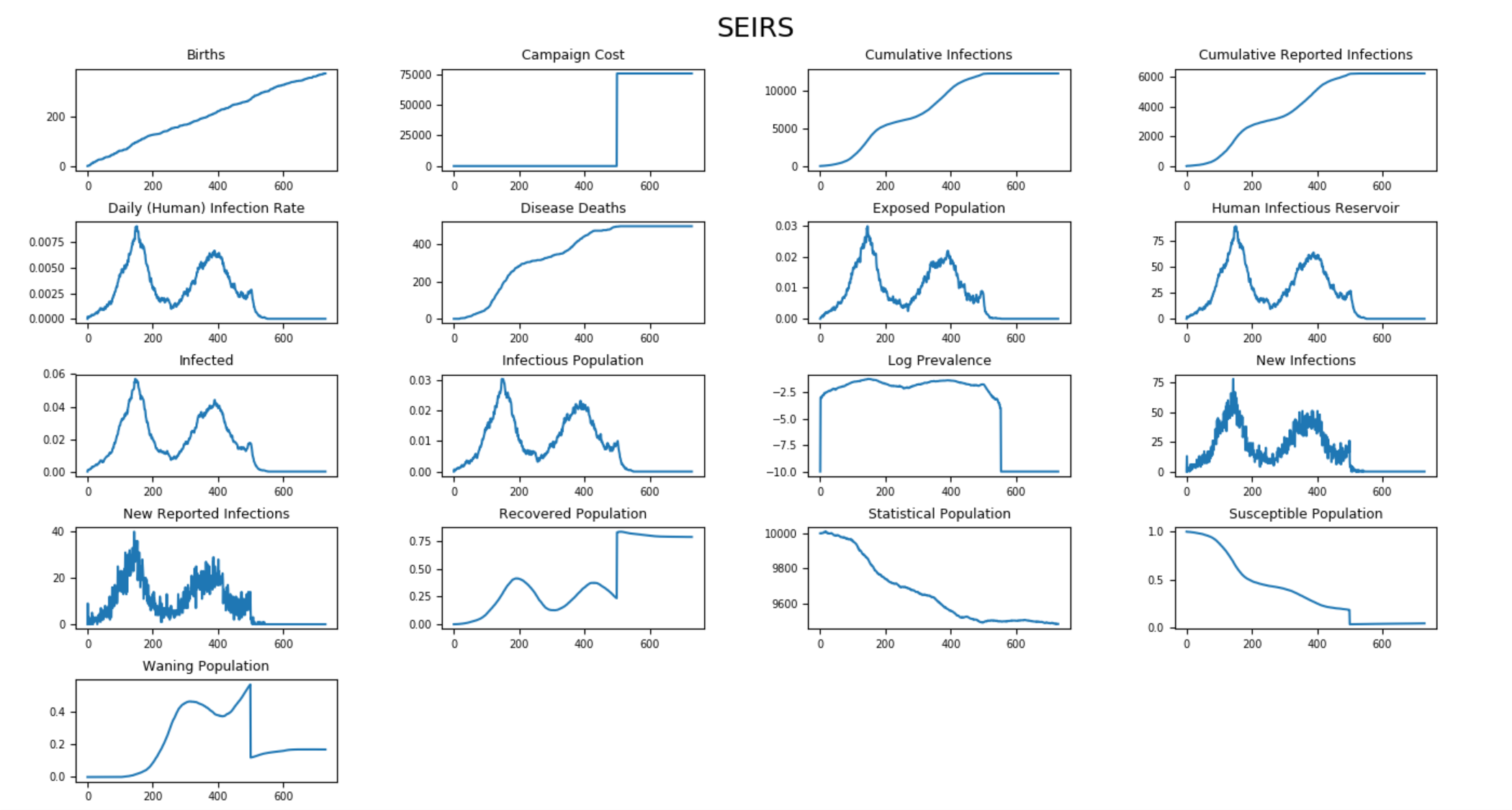
Figure 8: All output channels for SEIRS outbreak¶