T7 - Calibration

An interactive version of this notebook is available on Google Colab or Binder.

Disease models typically require contextualization to a relevant setting of interest prior to addressing “what-if” scenario questions. The process of tuning model input parameters so that model outputs match observed data is known as calibration. There are many approaches to model calibration, ranging from manual tuning to fully Bayesian methods.

For many applications, we have found that an optimization-based approach is sufficient. Such methods avoid the tedious process of manual tuning and are less computationally expensive than fully Bayesian methods. One such optimization-based approach is the Optuna library, which is a Bayesian hyperparameter optimization framework. Optuna is designed for tuning hyperparameters of machine learning models, but it can also be used to calibrate disease models.

Calibration libraries often treat the disease model as a black box, where the input parameters are the “hyperparameters” to be tuned. The calibration process is often iterative and requires a combination of expert knowledge and computational tools. The optimization algorithm iteratively chooses new parameter values to evaluate, and the model is run with these values to generate outputs. The outputs are compared to observed data, and a loss function is calculated to quantify the difference between the model outputs and the observed data. The optimization algorithm then uses this loss function to update its search strategy and choose new parameter values to evaluate. This process continues until the algorithm converges to a set of parameter values that minimize the loss function.

While many optimization algorithms are available, Starsim has a built-in interface to the Optuna library, which we will demonstrate in this tutorial. We will use a simple Susceptible-Infected-Recovered (SIR) model as an example. We will tune three input parameters, the infectivity parameter, beta, the initial prevalence parameter, init_prev, and the Poisson-distributed degree distribution parameter, n_contacts. We will calibrate the model using a beta-binomial likelihood function so as to match prevalence at three distinct time points.

We begin with a few imports and default settings:

#%% Imports and settings
import sciris as sc
import starsim as ss
import numpy as np
import pandas as pd
import matplotlib.dates as mdates

n_agents = 2e3
debug = False # If true, will run in serial

The calibration class will require a base Sim object. This sim will later be modified according to parameters selected by the optimization engine. The following function creates the base Sim object.

def make_sim():
    sir = ss.SIR(
        beta = ss.beta(0.075),
        init_prev = ss.bernoulli(0.02),
    )
    random = ss.RandomNet(n_contacts=ss.poisson(4))

    sim = ss.Sim(
        n_agents = n_agents,
        start = sc.date('2020-01-01'),
        stop = sc.date('2020-02-12'),
        dt = 1,
        unit = 'day',
        diseases = sir,
        networks = random,
        verbose = 0,
    )

    return sim

Now let’s define the calibration parameters. These are the inputs that Optuna will be able to modify. Here, we define three such parameters, beta, init_prev, and n_contacts.

Each parameter entry should have range defined by low and high as well as a guess values. The guess value is not used by Optuna, rather only for a check after calibration completes to see if the new parameters are better than the guess values.

You’ll notice there are a few other parameters that can be specified. For example, the data type of the parameter appears in suggest_type. Possible values are listed in the Optuna documentation, and include suggest_float for float values and suggest_int for integer types.

To make things easier for the search algorithm, it’s helpful to indicate how outputs are expected to change with inputs. For example, increasing beta from 0.01 to 0.02 should double disease transmission, but increasing from 0.11 to 0.12 will have a small effect. Thus, we indicate that this parameter should be calibrated with log=True.

# Define the calibration parameters
calib_pars = dict(
    beta = dict(low=0.01, high=0.30, guess=0.15, suggest_type='suggest_float', log=True), # Note the log scale
    init_prev = dict(low=0.01, high=0.05, guess=0.15), # Default type is suggest_float, no need to re-specify
    n_contacts = dict(low=2, high=10, guess=3, suggest_type='suggest_int'), # Suggest int just for this demo
)

The optimization engine iteratively chooses input parameters to simulate. Those parameters are passed into the following build_sim function as a dictionary of calib_pars along with the base sim and any other key word arguments. The calib_pars will be as above, but importantly will have an additional key named value containing the value selected by Optuna.

When modifying a sim, it is important to realize that the simulation has not been initialized yet. Nonetheless, the configuration is available for modification at sim.pars, as demonstrated in the function below for the SIR example.

def build_sim(sim, calib_pars, n_reps=1, **kwargs):
    """
    Modify the base simulation by applying calib_pars. The result can be a
    single simulation or multiple simulations if n_reps>1. Note that here we are
    simply building the simulation by modifying the base sim. Running the sims
    and extracting results will be done by the calibration function.
    """

    sir = sim.pars.diseases # There is only one disease in this simulation and it is a SIR
    net = sim.pars.networks # There is only one network in this simulation and it is a RandomNet

    for k, pars in calib_pars.items(): # Loop over the calibration parameters
        if k == 'rand_seed':
            sim.pars.rand_seed = v
            continue

        # Each item in calib_pars is a dictionary with keys like 'low', 'high',
        # 'guess', 'suggest_type', and importantly 'value'. The 'value' key is
        # the one we want to use as that's the one selected by the algorithm
        v = pars['value']
        if k == 'beta':
            sir.pars.beta = ss.beta(v)
        elif k == 'init_prev':
            sir.pars.init_prev = ss.bernoulli(v)
        elif k == 'n_contacts':
            net.pars.n_contacts = ss.poisson(v)
        else:
            raise NotImplementedError(f'Parameter {k} not recognized')

    # If just one simulation per parameter set, return the single simulation
    if n_reps == 1:
        return sim

    # But if you'd like to run multiple simulations with the same parameters, we return a MultiSim instead
    # Note that each simulation will have a different random seed, you can set specific seeds if you like
    # Also note that parallel=False and debug=True are important to avoid issues with parallelism in the calibration
    # Advanced: If running multiple reps, you can choose if/how they are combined using the "combine_reps" argument to each CalibComponent, introduced below.
    ms = ss.MultiSim(sim, iterpars=dict(rand_seed=np.random.randint(0, 1e6, n_reps)), initialize=True, debug=True, parallel=False)
    return ms

The Starsim framework has been integrated with the Optuna hyperparameter optimization algorithm to facilitate calibration through the Calibration class. Recall that an optimization-based approach to calibration minimizes a function of the input parameters. This function is key to achieving an acceptable calibration.

There are two ways to describe the goodness-of-fit function for the Calibration. The first method is to directly provide a function that the algorithm will call. The eval_fn will be passed each completed sim after running, and is expected to return a float representing the mismatch (lower is better as the optimization algorithm is configured to minimize). Data can be passed into the eval_fn via eval_kwargs.

As an alternative to directly specifying the evaluation function, you can use CalibComponents. Each component includes real data, for example from a survey, that is compared against simulation data from the model. Several components and be used at the same time, for example one for disease prevalence and another for treatment coverage. Each component computes a likelihood of the data given the input parameters, as assessed via simulation. Components are combined assuming independence.

The base class for a component is called CalibComponent, which you can use to define your own likelihood. However, we have provided components for several key likelihood functions including BetaBinomial, Binomial, DirichletMultinomial, GammaPoisson, and Normal. The Normal component is most like a traditional squared error. Each component takes in a name and a weight, which is used when combining log likelihoods.

Importantly, each component takes in the calibration target, the real data that was observed, in an argument called expected. This argument should be a Pandas Dataframe with one row per time point and columns that will depend on the specific component type. For example, the Binomial component requires columns of n (trials) and x (successes).

The components also handle extracting data from each simulation using the extract_fn argument. The value of this argument should be a function that takes in a simulation and returns a Pandas DataFrame. The specifics of the columns will depend a bit on the type of component (e.g. BetaBinomial is different from Normal), but often looks like a simulated version of expected. We will see examples below.

We’ll also see how to use the conform argument, the purpose of which is to temporally align the simulation output to the real data. This argument works along with the extract_fn to produce the final simulation outputs that are used in the likelihood function. The conformer is a function that takes in the expected data you provided and the actual simulation result the comes out of the extract_fn. The conformers we have built in are as follows:

• step_containing: Conform by simply choosing the simulated timestep that contains the time indicated in the real data (expected)

• prevalent: Interpolate the simulated timepoints to estimate the values that would have occurred at each real timepoint

• incident: While the two methods above capture the state of the model at a particular point in time (stocks), this component allows you to capture the behavior of the model over time (flows). Instead of just giving one time value, t, you’ll provide a second time value as well called t1. This conformer will add up events occurring between the two time points.

Let’s make a Binomial component, as might be used to calibrate disease prevalence.

prevalence = ss.Normal(
    name = 'Disease prevalence',
    conform = 'prevalent',

    expected = pd.DataFrame({
        'x': [0.13, 0.16, 0.06],    # Prevalence of infection
    }, index=pd.Index([ss.date(d) for d in ['2020-01-12', '2020-01-25', '2020-02-02']], name='t')), # On these dates

    extract_fn = lambda sim: pd.DataFrame({
        'x': sim.results.sir.prevalence,
    }, index=pd.Index(sim.results.timevec, name='t')),

    # You can specify the variance as well, but it's optional (max likelihood estimates will be used if not provided)
    # This could be a single float or an array with the same shape as the expected values
    sigma2 = 0.05, # e.g. (num_replicates/sigma2_model + 1/sigma2_data)^-1
    #sigma2 = np.array([0.05, 0.25, 0.01])
)

Finally, we can bring all the pieces together. We make a single base simulation and create an instance of a Starsim Calibration object. This object requires a few arguments, like the calib_pars and sim. We also pass in the function that modifies the base sim, here our build_sim function. No additional build_kw are required in this example.

We also pass in a list of components. Instead of using this “component-based” system, a user could simply provide an eval_fn, which takes in a completed sim an any eval_kwargs and returns a “mismatch” score to be minimized.

We can also specify the total number of trials to run, the number of parallel works, and a few other parameters.

sc.heading('Beginning calibration')

# Make the sim and data
sim = make_sim()

# Make the calibration
calib = ss.Calibration(
    calib_pars = calib_pars,
    sim = sim,
    build_fn = build_sim,
    build_kw = dict(n_reps=3), # Run 3 replicates for each parameter set
    reseed = True, # If true, a different random seed will be provided to each configuration
    components = [prevalence],
    total_trials = 100,
    n_workers = None, # None indicates to use all available CPUs
    die = True,
    debug = debug, # Run in serial if True
)

# Perform the calibration
sc.printcyan('\nPeforming calibration...')
calib.calibrate();

—————————————————————
Beginning calibration
—————————————————————


Peforming calibration...
Removed existing calibration file starsim_calibration.db
sqlite:///starsim_calibration.db

[I 2025-02-26 01:57:58,425] A new study created in RDB with name: starsim_calibration

Elapsed time: 0.731 s
Elapsed time: 0.765 s

[I 2025-02-26 01:57:59,799] Trial 1 finished with value: -0.3020779464066088 and parameters: {'beta': 0.1272947245094346, 'init_prev': 0.04936160666855756, 'n_contacts': 3, 'rand_seed': 894722}. Best is trial 0 with value: -0.46927727601420205.
[I 2025-02-26 01:57:59,802] Trial 0 finished with value: -0.46927727601420205 and parameters: {'beta': 0.13744412355576108, 'init_prev': 0.035521729333525695, 'n_contacts': 9, 'rand_seed': 884946}. Best is trial 0 with value: -0.46927727601420205.

Elapsed time: 0.685 s

[I 2025-02-26 01:58:00,594] Trial 2 finished with value: -0.4362976117060988 and parameters: {'beta': 0.01877193887154933, 'init_prev': 0.04789759021382037, 'n_contacts': 4, 'rand_seed': 699509}. Best is trial 0 with value: -0.46927727601420205.

Elapsed time: 0.726 s

[I 2025-02-26 01:58:00,654] Trial 3 finished with value: -0.3337693410343425 and parameters: {'beta': 0.1549214463557853, 'init_prev': 0.01782949861788227, 'n_contacts': 8, 'rand_seed': 369728}. Best is trial 0 with value: -0.46927727601420205.

Elapsed time: 0.687 s

[I 2025-02-26 01:58:01,393] Trial 4 finished with value: -0.43592250849386527 and parameters: {'beta': 0.02150103058093407, 'init_prev': 0.013545198973503503, 'n_contacts': 5, 'rand_seed': 800831}. Best is trial 0 with value: -0.46927727601420205.

Elapsed time: 0.729 s

[I 2025-02-26 01:58:01,497] Trial 5 finished with value: -0.4574505678798132 and parameters: {'beta': 0.019225200494805323, 'init_prev': 0.028999606265160405, 'n_contacts': 7, 'rand_seed': 408067}. Best is trial 0 with value: -0.46927727601420205.

Elapsed time: 0.726 s

[I 2025-02-26 01:58:02,238] Trial 6 finished with value: 0.10086158225914274 and parameters: {'beta': 0.09103160910336534, 'init_prev': 0.036113196088750237, 'n_contacts': 6, 'rand_seed': 596519}. Best is trial 0 with value: -0.46927727601420205.

Elapsed time: 0.801 s

[I 2025-02-26 01:58:02,409] Trial 7 finished with value: -0.5167985646805622 and parameters: {'beta': 0.018291014311647678, 'init_prev': 0.03237231057911513, 'n_contacts': 10, 'rand_seed': 213515}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.746 s

[I 2025-02-26 01:58:03,291] Trial 8 finished with value: -0.4403995564018168 and parameters: {'beta': 0.014505674925162602, 'init_prev': 0.017847606319699436, 'n_contacts': 9, 'rand_seed': 335264}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.953 s

[I 2025-02-26 01:58:03,481] Trial 9 finished with value: -0.46501565612758217 and parameters: {'beta': 0.018513692312104067, 'init_prev': 0.042895952010381024, 'n_contacts': 8, 'rand_seed': 729223}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.783 s

[I 2025-02-26 01:58:04,193] Trial 10 finished with value: -0.516786205599527 and parameters: {'beta': 0.025434571100905898, 'init_prev': 0.030904738475883126, 'n_contacts': 8, 'rand_seed': 856346}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.795 s

[I 2025-02-26 01:58:04,418] Trial 11 finished with value: -0.27472607813655425 and parameters: {'beta': 0.04282629665492087, 'init_prev': 0.027183096393455716, 'n_contacts': 10, 'rand_seed': 29622}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.797 s

[I 2025-02-26 01:58:05,133] Trial 12 finished with value: -0.24669808533005766 and parameters: {'beta': 0.04310936020789816, 'init_prev': 0.027747510001602645, 'n_contacts': 10, 'rand_seed': 23975}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.795 s

[I 2025-02-26 01:58:05,354] Trial 13 finished with value: -0.2912847852793401 and parameters: {'beta': 0.04084649066793609, 'init_prev': 0.02443528639247514, 'n_contacts': 10, 'rand_seed': 129964}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.720 s

[I 2025-02-26 01:58:05,995] Trial 14 finished with value: -0.43213158570570065 and parameters: {'beta': 0.010576885539333824, 'init_prev': 0.035954462339671166, 'n_contacts': 7, 'rand_seed': 212664}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.708 s

[I 2025-02-26 01:58:06,202] Trial 15 finished with value: -0.43088204290531096 and parameters: {'beta': 0.010278885375668208, 'init_prev': 0.03577279695384914, 'n_contacts': 7, 'rand_seed': 991956}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.716 s

[I 2025-02-26 01:58:06,857] Trial 16 finished with value: -0.4475182361881893 and parameters: {'beta': 0.26537693054928496, 'init_prev': 0.0412476247527066, 'n_contacts': 8, 'rand_seed': 540785}. Best is trial 7 with value: -0.5167985646805622.

Elapsed time: 0.795 s

[I 2025-02-26 01:58:07,143] Trial 17 finished with value: -0.5775133319374116 and parameters: {'beta': 0.03174345981741847, 'init_prev': 0.022731642636282395, 'n_contacts': 9, 'rand_seed': 537883}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.794 s

[I 2025-02-26 01:58:07,802] Trial 18 finished with value: -0.5648006902736421 and parameters: {'beta': 0.02847400160304969, 'init_prev': 0.022370835466892385, 'n_contacts': 9, 'rand_seed': 269698}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.641 s

[I 2025-02-26 01:58:07,940] Trial 19 finished with value: -0.4286678092222963 and parameters: {'beta': 0.031245819532279857, 'init_prev': 0.021011582707485425, 'n_contacts': 2, 'rand_seed': 226103}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.646 s

[I 2025-02-26 01:58:08,605] Trial 20 finished with value: -0.445758676340612 and parameters: {'beta': 0.06448667584218315, 'init_prev': 0.020416583683927125, 'n_contacts': 2, 'rand_seed': 434185}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.745 s

[I 2025-02-26 01:58:08,844] Trial 21 finished with value: -0.55713695081185 and parameters: {'beta': 0.06050417136257938, 'init_prev': 0.011191883542687964, 'n_contacts': 6, 'rand_seed': 430827}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.783 s

[I 2025-02-26 01:58:09,550] Trial 22 finished with value: -0.5572429497535192 and parameters: {'beta': 0.0287360546592158, 'init_prev': 0.01157713643202411, 'n_contacts': 9, 'rand_seed': 271527}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.740 s

[I 2025-02-26 01:58:09,742] Trial 23 finished with value: -0.553488038709627 and parameters: {'beta': 0.06581849637820003, 'init_prev': 0.011104887206213637, 'n_contacts': 5, 'rand_seed': 601221}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.792 s

[I 2025-02-26 01:58:10,503] Trial 24 finished with value: -0.559705859817331 and parameters: {'beta': 0.030706437056212902, 'init_prev': 0.014488651814131009, 'n_contacts': 9, 'rand_seed': 282393}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.793 s

[I 2025-02-26 01:58:10,695] Trial 25 finished with value: -0.5728354632652303 and parameters: {'beta': 0.030327227454660502, 'init_prev': 0.015366648141657974, 'n_contacts': 9, 'rand_seed': 300065}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.793 s

[I 2025-02-26 01:58:11,461] Trial 26 finished with value: -0.5739799250966252 and parameters: {'beta': 0.03384119854587671, 'init_prev': 0.015377515034246248, 'n_contacts': 9, 'rand_seed': 512978}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.786 s

[I 2025-02-26 01:58:11,641] Trial 27 finished with value: -0.55664843884958 and parameters: {'beta': 0.035768553923902664, 'init_prev': 0.022826418749857667, 'n_contacts': 9, 'rand_seed': 497214}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.758 s

[I 2025-02-26 01:58:12,379] Trial 28 finished with value: -0.5548047630832023 and parameters: {'beta': 0.04633508750992675, 'init_prev': 0.016564180599868483, 'n_contacts': 7, 'rand_seed': 500874}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.763 s

[I 2025-02-26 01:58:12,564] Trial 29 finished with value: -0.5285085464217812 and parameters: {'beta': 0.04994911080299641, 'init_prev': 0.017149415946674938, 'n_contacts': 7, 'rand_seed': 505712}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.760 s

[I 2025-02-26 01:58:13,304] Trial 30 finished with value: -0.34246801511051533 and parameters: {'beta': 0.05606201322508482, 'init_prev': 0.015777877148690892, 'n_contacts': 8, 'rand_seed': 657210}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.733 s

[I 2025-02-26 01:58:13,456] Trial 31 finished with value: 0.4069139337988642 and parameters: {'beta': 0.08068164623910336, 'init_prev': 0.014101705361799336, 'n_contacts': 8, 'rand_seed': 627098}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.786 s

[I 2025-02-26 01:58:14,255] Trial 32 finished with value: -0.5456187310971692 and parameters: {'beta': 0.02490280419042953, 'init_prev': 0.024602970304479103, 'n_contacts': 9, 'rand_seed': 117858}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.783 s

[I 2025-02-26 01:58:14,399] Trial 33 finished with value: -0.5358000279498918 and parameters: {'beta': 0.024498495763057203, 'init_prev': 0.02462239531520946, 'n_contacts': 9, 'rand_seed': 354630}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.773 s

[I 2025-02-26 01:58:15,191] Trial 34 finished with value: -0.4508458689628946 and parameters: {'beta': 0.015165922963232898, 'init_prev': 0.020656891834724314, 'n_contacts': 10, 'rand_seed': 343546}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.770 s

[I 2025-02-26 01:58:15,330] Trial 35 finished with value: -0.45257768238168683 and parameters: {'beta': 0.014207873863626043, 'init_prev': 0.019887443183486477, 'n_contacts': 10, 'rand_seed': 294759}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.801 s

[I 2025-02-26 01:58:16,154] Trial 36 finished with value: -0.5409460432894567 and parameters: {'beta': 0.03384628926967535, 'init_prev': 0.01911779761412526, 'n_contacts': 10, 'rand_seed': 554786}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.787 s

[I 2025-02-26 01:58:16,278] Trial 37 finished with value: -0.5540346187963487 and parameters: {'beta': 0.035334476891536994, 'init_prev': 0.023182670887483867, 'n_contacts': 9, 'rand_seed': 138527}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.778 s
Elapsed time: 0.659 s

[I 2025-02-26 01:58:17,086] Trial 38 finished with value: -0.5540912711354693 and parameters: {'beta': 0.03709611984895041, 'init_prev': 0.02215204557679748, 'n_contacts': 9, 'rand_seed': 722429}. Best is trial 17 with value: -0.5775133319374116.
[I 2025-02-26 01:58:17,103] Trial 39 finished with value: -0.4279528813501005 and parameters: {'beta': 0.020849002645476893, 'init_prev': 0.013384792708315368, 'n_contacts': 3, 'rand_seed': 446821}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.725 s
Elapsed time: 0.742 s

[I 2025-02-26 01:58:17,994] Trial 41 finished with value: 0.2635266278790584 and parameters: {'beta': 0.10147716185968209, 'init_prev': 0.026469917807745262, 'n_contacts': 6, 'rand_seed': 460600}. Best is trial 17 with value: -0.5775133319374116.
[I 2025-02-26 01:58:18,033] Trial 40 finished with value: -0.051320813549925424 and parameters: {'beta': 0.07919380168384392, 'init_prev': 0.025795671607265515, 'n_contacts': 6, 'rand_seed': 405105}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.782 s

[I 2025-02-26 01:58:18,924] Trial 42 finished with value: -0.5256660132854448 and parameters: {'beta': 0.028443857346200585, 'init_prev': 0.01525921160537563, 'n_contacts': 8, 'rand_seed': 385511}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.796 s

[I 2025-02-26 01:58:19,041] Trial 43 finished with value: -0.5541102675567049 and parameters: {'beta': 0.02828904669436415, 'init_prev': 0.012944641207037491, 'n_contacts': 9, 'rand_seed': 285845}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.785 s

[I 2025-02-26 01:58:19,890] Trial 44 finished with value: -0.47605999113068403 and parameters: {'beta': 0.022120429608822004, 'init_prev': 0.012799550237809099, 'n_contacts': 9, 'rand_seed': 300279}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.791 s

[I 2025-02-26 01:58:19,997] Trial 45 finished with value: -0.5009165409736223 and parameters: {'beta': 0.02203977958049053, 'init_prev': 0.018733346102868968, 'n_contacts': 9, 'rand_seed': 191898}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.744 s

[I 2025-02-26 01:58:20,794] Trial 46 finished with value: -0.44745194598524723 and parameters: {'beta': 0.01815375665569894, 'init_prev': 0.01857057377432058, 'n_contacts': 8, 'rand_seed': 170513}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.754 s

[I 2025-02-26 01:58:20,913] Trial 47 finished with value: -0.45539351390917965 and parameters: {'beta': 0.017796285124841205, 'init_prev': 0.03190091210906176, 'n_contacts': 8, 'rand_seed': 82633}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.768 s

[I 2025-02-26 01:58:21,727] Trial 48 finished with value: -0.533045199970548 and parameters: {'beta': 0.03880424013624795, 'init_prev': 0.03031071820881201, 'n_contacts': 8, 'rand_seed': 79991}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.797 s

[I 2025-02-26 01:58:21,875] Trial 49 finished with value: -0.5459740156442497 and parameters: {'beta': 0.0400475705100069, 'init_prev': 0.01005623347752357, 'n_contacts': 10, 'rand_seed': 245844}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.780 s

[I 2025-02-26 01:58:22,672] Trial 50 finished with value: -0.27608634854004177 and parameters: {'beta': 0.04920892632158244, 'init_prev': 0.010299528808113231, 'n_contacts': 10, 'rand_seed': 260991}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.787 s

[I 2025-02-26 01:58:22,827] Trial 51 finished with value: -0.1267245597569512 and parameters: {'beta': 0.04883297729295211, 'init_prev': 0.01491229355376645, 'n_contacts': 10, 'rand_seed': 323280}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.782 s

[I 2025-02-26 01:58:23,618] Trial 52 finished with value: -0.5672087549549869 and parameters: {'beta': 0.02996875924959594, 'init_prev': 0.014875381545346116, 'n_contacts': 9, 'rand_seed': 328697}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.786 s

[I 2025-02-26 01:58:23,777] Trial 53 finished with value: -0.569518007807931 and parameters: {'beta': 0.03065048543214196, 'init_prev': 0.012298317972853768, 'n_contacts': 9, 'rand_seed': 369020}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.784 s

[I 2025-02-26 01:58:24,571] Trial 54 finished with value: -0.5681046962755134 and parameters: {'beta': 0.030395640324410708, 'init_prev': 0.01600608164969504, 'n_contacts': 9, 'rand_seed': 555161}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.790 s

[I 2025-02-26 01:58:24,730] Trial 55 finished with value: -0.538962071415551 and parameters: {'beta': 0.025849948775767052, 'init_prev': 0.017320132589964333, 'n_contacts': 9, 'rand_seed': 384209}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.770 s

[I 2025-02-26 01:58:25,506] Trial 56 finished with value: -0.5667951795940208 and parameters: {'beta': 0.032809426316045616, 'init_prev': 0.016503259315542463, 'n_contacts': 8, 'rand_seed': 544008}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.780 s

[I 2025-02-26 01:58:25,680] Trial 57 finished with value: -0.564850866935907 and parameters: {'beta': 0.032897256075709994, 'init_prev': 0.012392938932051012, 'n_contacts': 8, 'rand_seed': 778030}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.733 s

[I 2025-02-26 01:58:26,406] Trial 58 finished with value: -0.4756897070544562 and parameters: {'beta': 0.21495061155970804, 'init_prev': 0.01233820557907152, 'n_contacts': 10, 'rand_seed': 793358}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.793 s

[I 2025-02-26 01:58:26,642] Trial 59 finished with value: -0.48304519893193365 and parameters: {'beta': 0.016137205876603177, 'init_prev': 0.03808807744224294, 'n_contacts': 10, 'rand_seed': 583268}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.959 s

[I 2025-02-26 01:58:27,535] Trial 60 finished with value: -0.5080176993285942 and parameters: {'beta': 0.02531324170277668, 'init_prev': 0.03877161290009804, 'n_contacts': 7, 'rand_seed': 573739}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.967 s

[I 2025-02-26 01:58:27,778] Trial 61 finished with value: -0.5455022807173983 and parameters: {'beta': 0.043724715167237097, 'init_prev': 0.028678448330868227, 'n_contacts': 7, 'rand_seed': 469245}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.786 s

[I 2025-02-26 01:58:28,485] Trial 62 finished with value: -0.46294311553976175 and parameters: {'beta': 0.042642873342462986, 'init_prev': 0.016361273772821386, 'n_contacts': 9, 'rand_seed': 512500}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.802 s

[I 2025-02-26 01:58:28,747] Trial 63 finished with value: -0.5722355510585154 and parameters: {'beta': 0.031169868442160124, 'init_prev': 0.015574225826280142, 'n_contacts': 9, 'rand_seed': 531259}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.787 s

[I 2025-02-26 01:58:29,438] Trial 64 finished with value: -0.5507962890004241 and parameters: {'beta': 0.031118047918408852, 'init_prev': 0.04982078878006651, 'n_contacts': 8, 'rand_seed': 664535}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.792 s

[I 2025-02-26 01:58:29,706] Trial 65 finished with value: -0.5337785384949022 and parameters: {'beta': 0.029376342187165307, 'init_prev': 0.048611517910786925, 'n_contacts': 9, 'rand_seed': 657950}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.788 s

[I 2025-02-26 01:58:30,394] Trial 66 finished with value: -0.5030528170529223 and parameters: {'beta': 0.023134548746609526, 'init_prev': 0.01434802339688624, 'n_contacts': 9, 'rand_seed': 624583}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.689 s

[I 2025-02-26 01:58:30,562] Trial 67 finished with value: -0.43334598040253564 and parameters: {'beta': 0.020401979746613303, 'init_prev': 0.014120930888736463, 'n_contacts': 5, 'rand_seed': 610149}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.664 s

[I 2025-02-26 01:58:31,228] Trial 68 finished with value: -0.42892315862663755 and parameters: {'beta': 0.020335294323745184, 'init_prev': 0.018319484768151685, 'n_contacts': 4, 'rand_seed': 416388}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.765 s

[I 2025-02-26 01:58:31,498] Trial 69 finished with value: -0.160214433433172 and parameters: {'beta': 0.05396359812116616, 'init_prev': 0.015504128899674723, 'n_contacts': 9, 'rand_seed': 468574}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.770 s

[I 2025-02-26 01:58:32,168] Trial 70 finished with value: -0.29304011653302875 and parameters: {'beta': 0.05542884172450322, 'init_prev': 0.01166252403951968, 'n_contacts': 9, 'rand_seed': 477886}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.794 s

[I 2025-02-26 01:58:32,461] Trial 71 finished with value: -0.5212173918466014 and parameters: {'beta': 0.026468153161629884, 'init_prev': 0.011455546261018712, 'n_contacts': 9, 'rand_seed': 327275}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.787 s

[I 2025-02-26 01:58:33,122] Trial 72 finished with value: -0.5741303752473317 and parameters: {'beta': 0.034461896575073245, 'init_prev': 0.016630263443686802, 'n_contacts': 8, 'rand_seed': 533914}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.778 s

[I 2025-02-26 01:58:33,410] Trial 73 finished with value: -0.5751285692639285 and parameters: {'beta': 0.033950119360976846, 'init_prev': 0.017227778647960653, 'n_contacts': 8, 'rand_seed': 558899}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.790 s

[I 2025-02-26 01:58:34,083] Trial 74 finished with value: -0.5276061723705863 and parameters: {'beta': 0.03616893952408826, 'init_prev': 0.021516930973696, 'n_contacts': 9, 'rand_seed': 533030}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.782 s

[I 2025-02-26 01:58:34,362] Trial 75 finished with value: -0.5766439552636444 and parameters: {'beta': 0.03715623331881709, 'init_prev': 0.019757615893116733, 'n_contacts': 8, 'rand_seed': 537228}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.786 s

[I 2025-02-26 01:58:35,036] Trial 76 finished with value: -0.5581088311486136 and parameters: {'beta': 0.038097581046719065, 'init_prev': 0.017588283257187292, 'n_contacts': 8, 'rand_seed': 521700}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.768 s

[I 2025-02-26 01:58:35,298] Trial 77 finished with value: -0.5692562937801686 and parameters: {'beta': 0.0390825757022443, 'init_prev': 0.017631604046138706, 'n_contacts': 7, 'rand_seed': 521905}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.780 s

[I 2025-02-26 01:58:35,988] Trial 78 finished with value: -0.5297078790810101 and parameters: {'beta': 0.04482237470631937, 'init_prev': 0.01979867715314302, 'n_contacts': 8, 'rand_seed': 580006}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.789 s

[I 2025-02-26 01:58:36,257] Trial 79 finished with value: -0.5651792878262675 and parameters: {'beta': 0.034290325367499284, 'init_prev': 0.02021801227104019, 'n_contacts': 8, 'rand_seed': 572264}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.788 s

[I 2025-02-26 01:58:36,946] Trial 80 finished with value: -0.5715638034115708 and parameters: {'beta': 0.03342903895001619, 'init_prev': 0.023466579442430465, 'n_contacts': 8, 'rand_seed': 687280}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.762 s

[I 2025-02-26 01:58:37,191] Trial 81 finished with value: -0.5441783061959649 and parameters: {'beta': 0.03285530338320188, 'init_prev': 0.019318518211276163, 'n_contacts': 7, 'rand_seed': 490730}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.765 s

[I 2025-02-26 01:58:37,882] Trial 82 finished with value: -0.48763406386997654 and parameters: {'beta': 0.02721518479909531, 'init_prev': 0.01937042805478145, 'n_contacts': 7, 'rand_seed': 691693}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.773 s

[I 2025-02-26 01:58:38,142] Trial 83 finished with value: -0.5138065503370074 and parameters: {'beta': 0.02703799206974642, 'init_prev': 0.02167206733198509, 'n_contacts': 8, 'rand_seed': 719519}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.773 s

[I 2025-02-26 01:58:38,827] Trial 84 finished with value: -0.4944128068648132 and parameters: {'beta': 0.02315490884708703, 'init_prev': 0.023254449763858983, 'n_contacts': 8, 'rand_seed': 631088}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.774 s

[I 2025-02-26 01:58:39,088] Trial 85 finished with value: -0.49295355817945435 and parameters: {'beta': 0.023363899521133834, 'init_prev': 0.02314488499462948, 'n_contacts': 8, 'rand_seed': 878379}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.776 s

[I 2025-02-26 01:58:39,780] Trial 86 finished with value: -0.5663967532656654 and parameters: {'beta': 0.03618721918756279, 'init_prev': 0.024079275843548482, 'n_contacts': 8, 'rand_seed': 757838}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.801 s

[I 2025-02-26 01:58:40,061] Trial 87 finished with value: -0.44645079552313877 and parameters: {'beta': 0.03994689903376177, 'init_prev': 0.0136826137960449, 'n_contacts': 10, 'rand_seed': 969269}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.803 s

[I 2025-02-26 01:58:40,755] Trial 88 finished with value: -0.4271562928458592 and parameters: {'beta': 0.0418535939784796, 'init_prev': 0.013555570742065362, 'n_contacts': 10, 'rand_seed': 438561}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.776 s

[I 2025-02-26 01:58:41,013] Trial 89 finished with value: -0.36872158004339917 and parameters: {'beta': 0.04595471218875057, 'init_prev': 0.020726300935840422, 'n_contacts': 9, 'rand_seed': 823783}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.796 s

[I 2025-02-26 01:58:41,726] Trial 90 finished with value: -0.5648249881764392 and parameters: {'beta': 0.031107722110704856, 'init_prev': 0.025836251476338747, 'n_contacts': 9, 'rand_seed': 405356}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.759 s

[I 2025-02-26 01:58:41,949] Trial 91 finished with value: 0.17216180822270688 and parameters: {'beta': 0.06216161541600637, 'init_prev': 0.025480338283852814, 'n_contacts': 9, 'rand_seed': 369186}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.771 s

[I 2025-02-26 01:58:42,674] Trial 92 finished with value: -0.5703597152627 and parameters: {'beta': 0.03813544662826084, 'init_prev': 0.017694498310998737, 'n_contacts': 7, 'rand_seed': 521156}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.772 s

[I 2025-02-26 01:58:42,898] Trial 93 finished with value: -0.5596408008513161 and parameters: {'beta': 0.03752640191408197, 'init_prev': 0.017950367715197535, 'n_contacts': 7, 'rand_seed': 521148}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.764 s

[I 2025-02-26 01:58:43,617] Trial 94 finished with value: -0.5486438839870338 and parameters: {'beta': 0.034193823343508484, 'init_prev': 0.017132051582531116, 'n_contacts': 7, 'rand_seed': 551886}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.754 s

[I 2025-02-26 01:58:43,828] Trial 95 finished with value: -0.5303462470302626 and parameters: {'beta': 0.033574325256913715, 'init_prev': 0.034398262377837635, 'n_contacts': 6, 'rand_seed': 547021}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.744 s

[I 2025-02-26 01:58:44,537] Trial 96 finished with value: -0.4908592357826895 and parameters: {'beta': 0.03201416937163534, 'init_prev': 0.016229683289695155, 'n_contacts': 6, 'rand_seed': 602141}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.770 s

[I 2025-02-26 01:58:44,779] Trial 97 finished with value: -0.5441403310443963 and parameters: {'beta': 0.028822745549680052, 'init_prev': 0.015178061474300114, 'n_contacts': 8, 'rand_seed': 502396}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.771 s

[I 2025-02-26 01:58:45,484] Trial 98 finished with value: -0.5225466130832469 and parameters: {'beta': 0.028088669708332202, 'init_prev': 0.015146038285452476, 'n_contacts': 8, 'rand_seed': 497375}. Best is trial 17 with value: -0.5775133319374116.

Elapsed time: 0.701 s

[I 2025-02-26 01:58:45,646] Trial 99 finished with value: -0.502353824462292 and parameters: {'beta': 0.024991904165243824, 'init_prev': 0.01848959884876774, 'n_contacts': 8, 'rand_seed': 680918}. Best is trial 17 with value: -0.5775133319374116.

Making results structure...
Processed 100 trials; 0 failed
Best pars: {'beta': 0.03174345981741847, 'init_prev': 0.022731642636282395, 'n_contacts': 9, 'rand_seed': 537883}
Removed existing calibration file starsim_calibration.db

Let’s look at the best parameters that were found. Note that the rand_seed was selected at random, but the other parameters are meaningful.

calib.best_pars

{'beta': 0.03174345981741847,
 'init_prev': 0.022731642636282395,
 'n_contacts': 9,
 'rand_seed': 537883}

Once the calibration is complete, we can compare the guess values to the best values found by calling check_fit.

# Confirm - Note the comparison is here configured over n_reps=15 replicates
sc.printcyan('\nConfirming fit...')

# Increase replicates to 15 for more representative results when running check_fit
calib.build_kw['n_reps'] = 15

calib.check_fit(do_plot=False)

Confirming fit...

Checking fit...
Elapsed time: 5.13 s
Fit with original pars: -0.3968508229570291
Fit with best-fit pars: -0.5706589661811614
✓ Calibration improved fit -0.3968508229570291 --> -0.5706589661811614

True

After calling check_fit, we can plot the results. This first plot shows the Normal likelihood distributions from each of the 15 simulations we did in check_fit as the colored lines. The vertical dashed line is located at the real (expected) data. Top row is the “guess” values and the bottom row is the new “best” parameters. We want the vertical dashed line to cross the Gaussians at high points, representing high likelihood.

calib.plot();

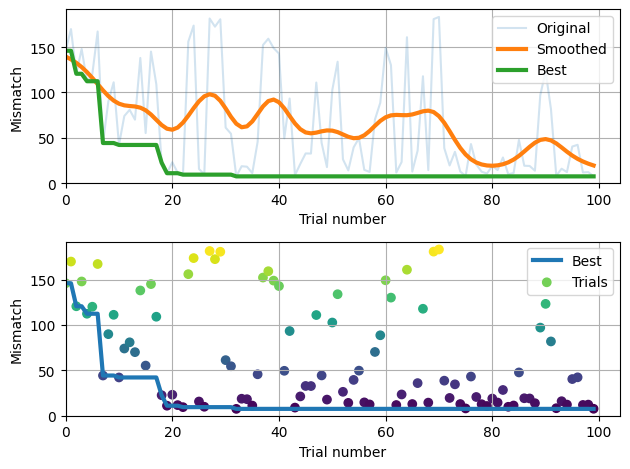
Another way to plot the results is via bootstrapping. Here we repeatedly choose 15 from the n_reps=15 simulations (with replacement), compute the average (or sum for some components), and repeatedly calculate the mean. We then plot the distribution of means, and hope it lands near the vertical dashed lines representing the real data.

calib.plot(bootstrap=True); # Pass bootstrap=True to produce this plot

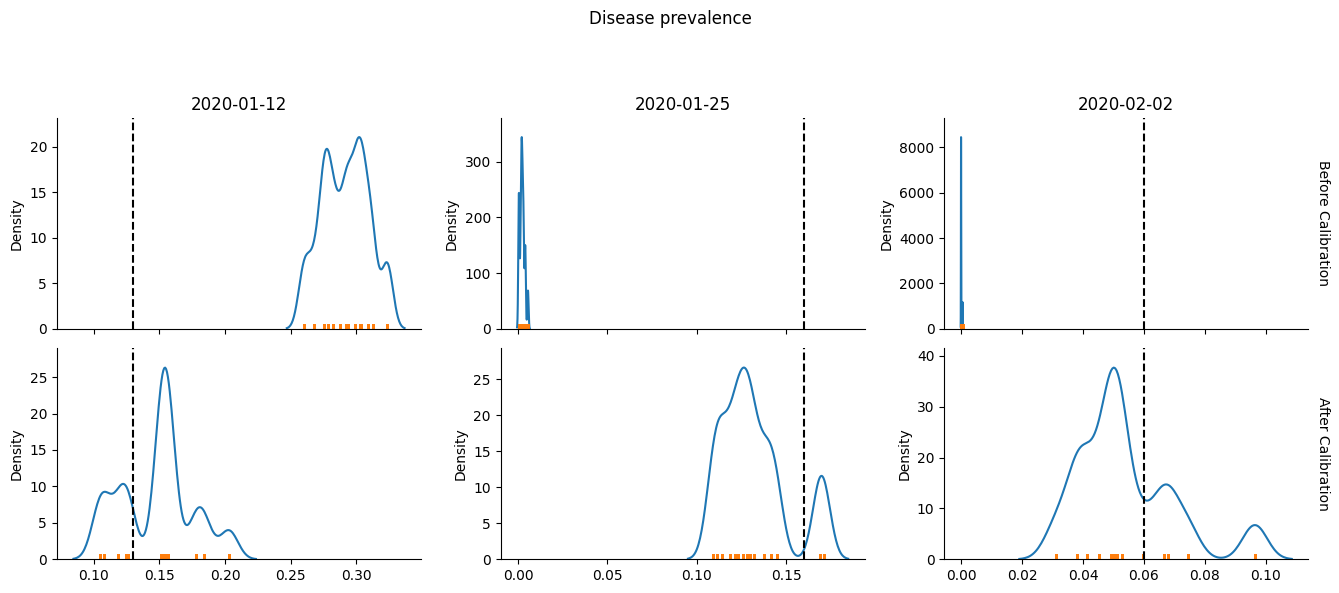
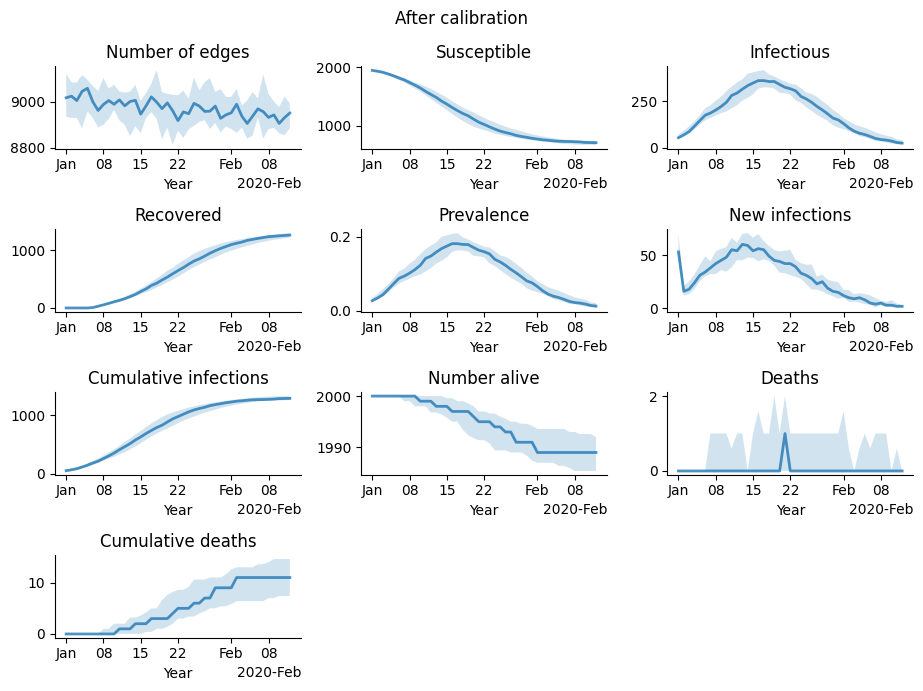
We can view some plots of the final fitted results. Whereas the two plots above were from the check_fit, running both “guess” and “best” parameters, here we make make new simulations to visualize the results.

g = calib.plot_final(); # Run the model for build_kw['n_reps'] = 15 replicates
for ax in g.axes: # Fix the date formatting
    ax.xaxis.set_major_formatter(mdates.ConciseDateFormatter(ax.xaxis.get_major_locator()))

Elapsed time: 2.53 s

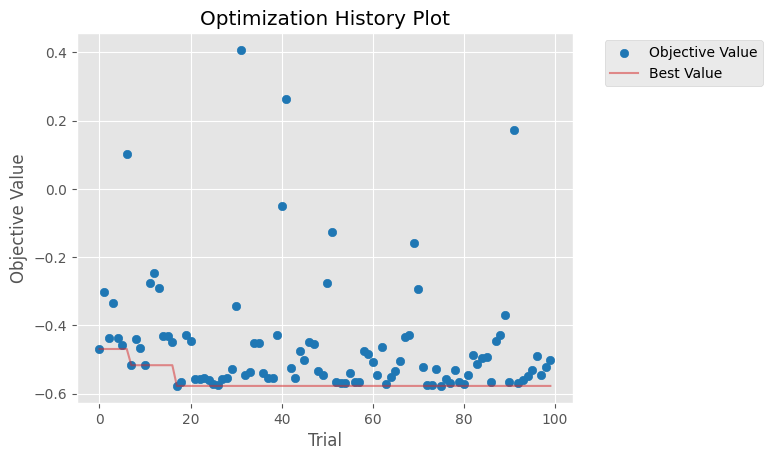
Optuna has lots of diagnostic plots that we can explore. Possible plots include:

• plot_contour

• plot_edf

• plot_hypervolume_history

• plot_intermediate_values

• plot_optimization_history

• plot_parallel_coordinate

• plot_param_importances

• plot_pareto_front

• plot_rank

• plot_slice

• plot_terminator_improvement

• plot_timeline

Here are some examples:

calib.plot_optuna('plot_optimization_history'); # Plot the optimization history

/home/docs/checkouts/readthedocs.org/user_builds/institute-for-disease-modeling-starsim/envs/latest/lib/python3.11/site-packages/starsim/calibration.py:434: ExperimentalWarning: plot_optimization_history is experimental (supported from v2.2.0). The interface can change in the future.
  fig = getattr(vis, method)(self.study)

calib.plot_optuna('plot_contour');

/home/docs/checkouts/readthedocs.org/user_builds/institute-for-disease-modeling-starsim/envs/latest/lib/python3.11/site-packages/starsim/calibration.py:434: ExperimentalWarning: plot_contour is experimental (supported from v2.2.0). The interface can change in the future.
  fig = getattr(vis, method)(self.study)
[W 2025-02-26 01:59:04,852] Output figures of this Matplotlib-based `plot_contour` function would be different from those of the Plotly-based `plot_contour`.

calib.plot_optuna('plot_param_importances');

Could not run plot_param_importances: Tried to import 'sklearn' but failed. Please make sure that the package is installed correctly to use this feature. Actual error: No module named 'sklearn'.

/home/docs/checkouts/readthedocs.org/user_builds/institute-for-disease-modeling-starsim/envs/latest/lib/python3.11/site-packages/starsim/calibration.py:434: ExperimentalWarning: plot_param_importances is experimental (supported from v2.2.0). The interface can change in the future.
  fig = getattr(vis, method)(self.study)

If you choose not to use components, you can always create your own mismatch function, as in the following example:

my_data = (ss.date('2020-01-12'), 0.13)

def eval(sim, expected):
    # Compute the squared error at one point in time.
    # expected will contain my_data in this example due to eval_kw
    date, p = expected
    if not isinstance(sim, ss.MultiSim):
        sim = ss.MultiSim(sims=[sim])

    ret = 0
    for s in sim.sims:
        ind = np.searchsorted(s.results.timevec, date, side='left')
        prev = s.results.sir.prevalence[ind]
        ret += (prev - p)**2
    return ret


# Define the calibration parameters
calib_pars = dict(
    beta = dict(low=0.01, high=0.30, guess=0.15, suggest_type='suggest_float', log=True),
)

# Make the sim and data
sim = make_sim()

# Make the calibration
calib = ss.Calibration(
    calib_pars = calib_pars,
    sim = sim,
    build_fn = build_sim,
    build_kw = dict(n_reps=2), # Two reps per point
    reseed = True,
    eval_fn = eval, # Will call my_function(msim, eval_kwargs)
    eval_kw = dict(expected=my_data), # Will call eval(sim, **eval_kw)
    total_trials = 10,
    n_workers = None, # None indicates to use all available CPUs
    die = True,
    debug = debug,
)

# Perform the calibration
sc.printcyan('\nPeforming calibration...')
calib.calibrate()

# Check
calib.check_fit()

Peforming calibration...
Removed existing calibration file starsim_calibration.db
sqlite:///starsim_calibration.db

[I 2025-02-26 01:59:07,441] A new study created in RDB with name: starsim_calibration

Elapsed time: 0.484 s
Elapsed time: 0.469 s

[I 2025-02-26 01:59:08,173] Trial 0 finished with value: 0.19783560672299205 and parameters: {'beta': 0.11169654390900886, 'rand_seed': 377571}. Best is trial 0 with value: 0.19783560672299205.
[I 2025-02-26 01:59:08,203] Trial 1 finished with value: 0.12104264538774273 and parameters: {'beta': 0.26997972714996227, 'rand_seed': 285469}. Best is trial 1 with value: 0.12104264538774273.

Elapsed time: 0.480 s

[I 2025-02-26 01:59:08,746] Trial 2 finished with value: 0.00996077788168722 and parameters: {'beta': 0.05398588480371177, 'rand_seed': 68995}. Best is trial 2 with value: 0.00996077788168722.

Elapsed time: 0.470 s

[I 2025-02-26 01:59:08,785] Trial 3 finished with value: 0.3876995723378762 and parameters: {'beta': 0.1404312435192579, 'rand_seed': 631873}. Best is trial 2 with value: 0.00996077788168722.

Elapsed time: 0.476 s

[I 2025-02-26 01:59:09,318] Trial 4 finished with value: 0.0074287828529071955 and parameters: {'beta': 0.053367773440311086, 'rand_seed': 347408}. Best is trial 4 with value: 0.0074287828529071955.

Elapsed time: 0.482 s

[I 2025-02-26 01:59:09,385] Trial 5 finished with value: 0.011457029615357956 and parameters: {'beta': 0.0511117685357763, 'rand_seed': 381536}. Best is trial 4 with value: 0.0074287828529071955.

Elapsed time: 0.446 s

[I 2025-02-26 01:59:09,854] Trial 6 finished with value: 0.030516495751877946 and parameters: {'beta': 0.022451710120833298, 'rand_seed': 153503}. Best is trial 4 with value: 0.0074287828529071955.

Elapsed time: 0.466 s

[I 2025-02-26 01:59:09,942] Trial 7 finished with value: 0.20572252302701596 and parameters: {'beta': 0.11372993597119885, 'rand_seed': 76837}. Best is trial 4 with value: 0.0074287828529071955.

Elapsed time: 0.473 s

[I 2025-02-26 01:59:10,424] Trial 8 finished with value: 0.01635627563656766 and parameters: {'beta': 0.044161232375820335, 'rand_seed': 893192}. Best is trial 4 with value: 0.0074287828529071955.

Elapsed time: 0.433 s

[I 2025-02-26 01:59:10,459] Trial 9 finished with value: 0.03213174575187794 and parameters: {'beta': 0.012823744086869834, 'rand_seed': 554866}. Best is trial 4 with value: 0.0074287828529071955.

Making results structure...
Processed 10 trials; 0 failed
Best pars: {'beta': 0.053367773440311086, 'rand_seed': 347408}
Removed existing calibration file starsim_calibration.db

Checking fit...
Elapsed time: 0.701 s
Fit with original pars: 0.4431622891697996
Fit with best-fit pars: 0.008422808196333058
✓ Calibration improved fit 0.4431622891697996 --> 0.008422808196333058

True

For more, take a look at test_calibration.py in the tests directory.