T7 - Calibration#

We saw in Tutorial 4 how to load and plot data. But the next step is to actually calibrate the model to the data, i.e. find the model parameters that are the most likely explanation for the observed data. This tutorial gives an introduction to the Fit object and some recipes for optimization approaches.

Click here to open an interactive version of this notebook.

The Fit object#

The Fit object is responsible for quantifying how well a given model run matches the data. Let’s consider a simple example, building on Tutorial 4:

[1]:

import covasim as cv
cv.options(jupyter=True, verbose=0)

pars = dict(
    pop_size  = 20_000,
    start_day = '2020-02-01',
    end_day   = '2020-04-11',
)
sim = cv.Sim(pars=pars, datafile='example_data.csv', interventions=cv.test_num(daily_tests='data'))
sim.run()
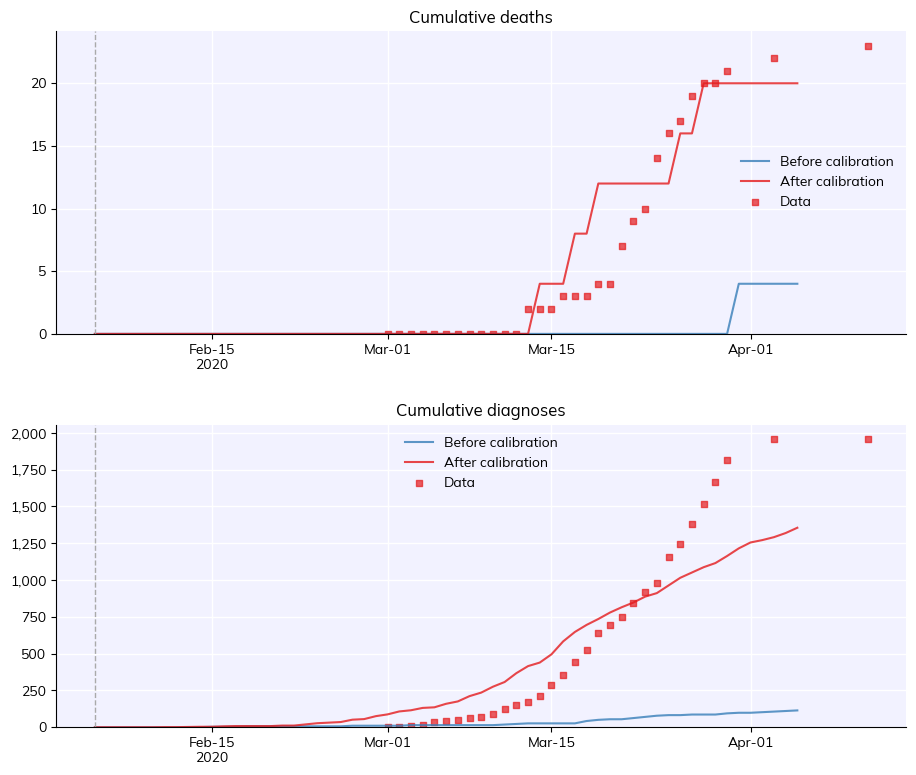
sim.plot(to_plot=['cum_tests', 'cum_diagnoses', 'cum_deaths'])

Covasim 3.1.7 (2026-02-18) — © 2020-2026 by IDM

../_images/tutorials_tut_calibration_3_1.png

We can see that tests match extremely well (they’re input data!), diagnoses match reasonably well, and deaths match poorly. Can the Fit object capture our intuition about this?

[2]:

fit = sim.compute_fit()
fit.summarize()

Mismatch values for:
#0. 'cum_deaths':    55.65217391304348
#1. 'cum_tests':     0.0
#2. 'cum_diagnoses': 22.428498467824312

Total mismatch value:
78.08067238086778

So the results seem to match our intuition. (Note that by default the Fit object uses normalized absolute difference, but other estimates, such as mean squared error, are also possible.)

What if we improve the fit? Does the mismatch reduce?

[3]:

sim['rel_death_prob'] = 2 # Increase the death rate since deaths were too low
sim.initialize(reset=True) # Reinitialize the sim

# Rerun and compute fit
sim.run()
fit = sim.compute_fit()

# Output
sim.plot(to_plot=['cum_tests', 'cum_diagnoses', 'cum_deaths'])

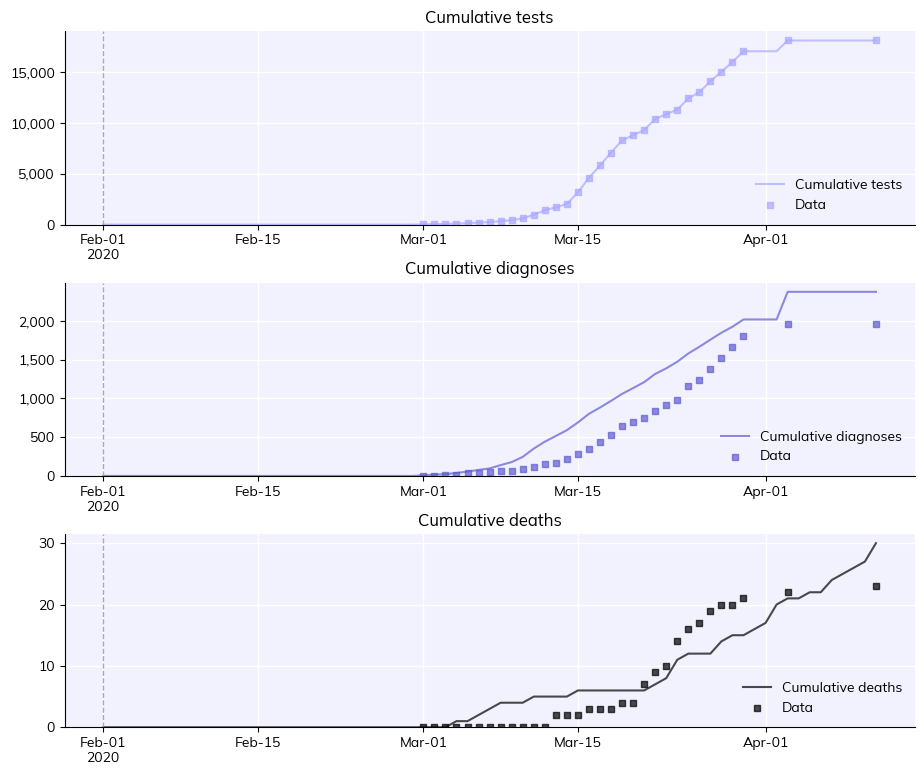
../_images/tutorials_tut_calibration_7_0.png

[4]:

fit.plot()
fit.summarize()

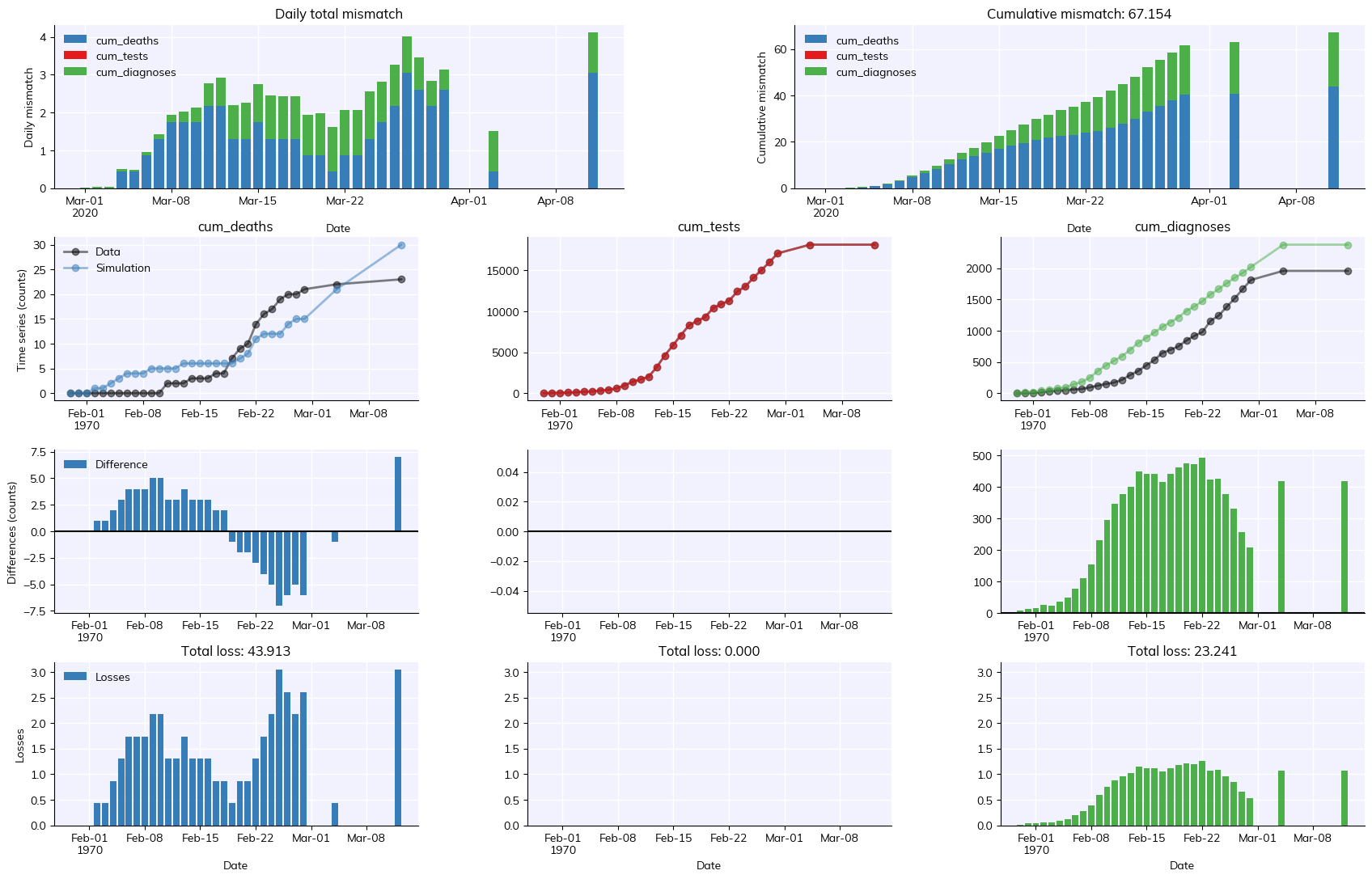
../_images/tutorials_tut_calibration_8_0.png

Mismatch values for:
#0. 'cum_deaths':    43.913043478260875
#1. 'cum_tests':     0.0
#2. 'cum_diagnoses': 23.240551583248212

Total mismatch value:
67.1535950615091

As expected, the fit is slightly improved. By now, you may be wondering how the mistmatch is actually calculated in Covasim. It follows more or less this expression:

\(\text{mismatch} = \sum_i\left(\sum_t\dfrac{|d_i(t) - m_i(t)|}{\text{max}(d_i(t))}\right)\)

where \(i\) is over different data quantities (eg, cum_tests, cum_deaths, cum_diagnoses in this example); \(t\) is time; \(d_i(t)\) is the time series of data for quantity \(i\) (the lines with square markers in the figures); and, \(m_i(t)\) is the time series of the model for quantity \(i\) (solid lines).

Each data quantity \(i\) has very different scales. Cumulative deaths could be in the few hundreds, while cumulative diagnoses could be in the tens of thousands (or more). For that reason we use the term \(\text{max}(d_i(t))\), so we can reasonably add individual mismatches of different quantities like cumulative deaths and diagnoses, to produce an overall mismatch, which is a ‘normalized’ absolute error of sorts.

Calibration approaches#

Calibration is a complex and dark art and cannot be covered fully here; many books have been written about it and it continues to be an area of active research. A good review article about calibrating agent-based models like Covasim is available here. Calibration is usually expressed as an optimization problem: specifically, find a vector of parameters θ that minimizes the mismatch between the data D and the model M(θ).

In practice, most calibration is done simply by hand, as in the example above. Once deaths are “calibrated”, the user might modify testing assumptions so that the diagnoses match. Since we are only fitting to deaths and diagnoses, the model is then “calibrated”.

However, automated approaches to calibration are possible as well. The simplest is probably the built-in SciPy optimization functions, e.g. scipy.optimize. A wrinkle here is that normal gradient descent methods will not work with Covasim or other agent-based models, due to the stochastic variability between model runs that makes the landscape very “bumpy”. One way of getting around this is to use many different runs and take the average, e.g.:

import covasim as cv
import numpy as np
from scipy import optimize

def objective(x, n_runs=10):
    print(f'Running sim for beta={x[0]}, rel_death_prob={x[1]}')
    pars = dict(
        pop_size       = 20_000,
        start_day      = '2020-02-01',
        end_day        = '2020-04-11',
        beta           = x[0],
        rel_death_prob = x[1],
        verbose        = 0,
    )
    sim = cv.Sim(pars=pars, datafile='example_data.csv', interventions=cv.test_num(daily_tests='data'))
    msim = cv.MultiSim(sim)
    msim.run(n_runs=n_runs)
    mismatches = []
    for sim in msim.sims:
        fit = sim.compute_fit()
        mismatches.append(fit.mismatch)
    mismatch = np.mean(mismatches)
    return mismatch

guess = [0.015, 1] # Initial guess of parameters -- beta and relative death probability
pars = optimize.minimize(objective, x0=guess, method='nelder-mead') # Run the optimization

This should converge after roughly 3-10 minutes, although you will likely find that the improvement is minimal.

What’s happening here? Trying to overcome the limitations of an algorithm that expects deterministic results simply by running more sims is fairly futile – if you run N sims and average them together, you’ve only reduced noise by √N, i.e. you have to average together 100 sims to reduce noise by a factor of 10, and even that might not be enough. Clearly, we need a more powerful approach.

Built-in calibration#

One such package we have found works reasonably well is called Optuna. It is built into Covasim as sim.calibrate() (it’s not installed by default, so please install it first with pip install optuna). Do not expect this to be a magic bullet solution: you will likely still need to try out multiple different parameter sets for calibration, manually update the values of uncalibrated parameters, check if the data actually make sense, etc. Even once all these things are in place, it still needs to be run for enough iterations, which might be a few hundred iterations for 3-4 calibrated (free) parameters or tens of thousands of iterations for 10 or more free parameters. The example below should get you started, but best to expect that it will not work for your particular use case without significant modification!

[5]:

'''
Example for running built-in calibration with Optuna
'''

import sciris as sc
import covasim as cv

# Create default simulation
pars = sc.objdict(
    pop_size       = 20_000,
    start_day      = '2020-02-01',
    end_day        = '2020-04-11',
    beta           = 0.015,
    rel_death_prob = 1.0,
    interventions  = cv.test_num(daily_tests='data'),
    verbose        = 0,
)
sim = cv.Sim(pars=pars, datafile='example_data.csv')

# Parameters to calibrate -- format is best, low, high
calib_pars = dict(
    beta           = [pars.beta, 0.005, 0.20],
    rel_death_prob = [pars.rel_death_prob, 0.5, 3.0],
)

if __name__ == '__main__':

    # Run the calibration
    calib = sim.calibrate(calib_pars=calib_pars, total_trials=100)

/home/docs/checkouts/readthedocs.org/user_builds/institute-for-disease-modeling-covasim/envs/latest/lib/python3.9/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

Could not delete study, skipping...
'Record does not exist.'
Removed existing calibration covasim_calibration.db

[I 2026-02-19 04:18:50,027] A new study created in RDB with name: covasim_calibration
[I 2026-02-19 04:18:50,981] Trial 0 finished with value: 714.2748812008704 and parameters: {'beta': 0.07086095118047508, 'rel_death_prob': 0.6442363057214155}. Best is trial 0 with value: 714.2748812008704.
[I 2026-02-19 04:18:51,048] Trial 1 finished with value: 2536.0021317226983 and parameters: {'beta': 0.19550623976161607, 'rel_death_prob': 2.0320913287964855}. Best is trial 0 with value: 714.2748812008704.
[I 2026-02-19 04:18:51,774] Trial 2 finished with value: 2533.1065417240306 and parameters: {'beta': 0.18824684567789718, 'rel_death_prob': 2.43944372313727}. Best is trial 0 with value: 714.2748812008704.
[I 2026-02-19 04:18:51,834] Trial 3 finished with value: 2454.8404538792915 and parameters: {'beta': 0.12549604895960895, 'rel_death_prob': 2.7478081362799913}. Best is trial 0 with value: 714.2748812008704.
[I 2026-02-19 04:18:52,463] Trial 4 finished with value: 816.1118266198872 and parameters: {'beta': 0.04044770274288666, 'rel_death_prob': 1.2320716644295038}. Best is trial 0 with value: 714.2748812008704.
[I 2026-02-19 04:18:52,552] Trial 5 finished with value: 1517.4218368343918 and parameters: {'beta': 0.060075891513222755, 'rel_death_prob': 1.6645086401773663}. Best is trial 0 with value: 714.2748812008704.
[I 2026-02-19 04:18:53,097] Trial 7 finished with value: 100.49662477239418 and parameters: {'beta': 0.014915935496619806, 'rel_death_prob': 2.060167846923509}. Best is trial 7 with value: 100.49662477239418.
[I 2026-02-19 04:18:53,115] Trial 6 finished with value: 727.1070746547055 and parameters: {'beta': 0.024861812044079997, 'rel_death_prob': 2.5332383692262517}. Best is trial 7 with value: 100.49662477239418.
[I 2026-02-19 04:18:53,821] Trial 9 finished with value: 423.09377359328505 and parameters: {'beta': 0.02772306739169366, 'rel_death_prob': 0.5477573242690201}. Best is trial 7 with value: 100.49662477239418.
[I 2026-02-19 04:18:53,885] Trial 8 finished with value: 1113.653128747169 and parameters: {'beta': 0.14235695909172197, 'rel_death_prob': 0.848024852915586}. Best is trial 7 with value: 100.49662477239418.
[I 2026-02-19 04:18:54,577] Trial 10 finished with value: 2231.069081138695 and parameters: {'beta': 0.12657933781131123, 'rel_death_prob': 2.178400305854648}. Best is trial 7 with value: 100.49662477239418.
[I 2026-02-19 04:18:54,642] Trial 11 finished with value: 1526.4672247635121 and parameters: {'beta': 0.08964658435839093, 'rel_death_prob': 1.8726176636265273}. Best is trial 7 with value: 100.49662477239418.
[I 2026-02-19 04:18:55,065] Trial 12 finished with value: 130.64318070790955 and parameters: {'beta': 0.00697738804412712, 'rel_death_prob': 1.4312847754674198}. Best is trial 7 with value: 100.49662477239418.
[I 2026-02-19 04:18:55,174] Trial 13 finished with value: 58.59128658347027 and parameters: {'beta': 0.013131530238586698, 'rel_death_prob': 1.4260865672750953}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:55,566] Trial 14 finished with value: 132.0178087667096 and parameters: {'beta': 0.006611949127650663, 'rel_death_prob': 1.3828378134893824}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:55,694] Trial 15 finished with value: 115.10836257050228 and parameters: {'beta': 0.010831672716564048, 'rel_death_prob': 1.3728347871517417}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:56,302] Trial 16 finished with value: 932.9797486343653 and parameters: {'beta': 0.0544307885358638, 'rel_death_prob': 1.0667132447385739}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:56,421] Trial 17 finished with value: 797.2851623218014 and parameters: {'beta': 0.04493474235368998, 'rel_death_prob': 0.9918125106381616}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:57,033] Trial 18 finished with value: 1504.2899809033177 and parameters: {'beta': 0.08580689199882781, 'rel_death_prob': 1.6751697733815534}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:57,158] Trial 19 finished with value: 1840.348403428521 and parameters: {'beta': 0.0906888031267339, 'rel_death_prob': 1.6649621473510892}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:57,833] Trial 20 finished with value: 2829.035506506195 and parameters: {'beta': 0.1691027308092879, 'rel_death_prob': 2.914225184151822}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:57,844] Trial 21 finished with value: 941.0234489496825 and parameters: {'beta': 0.027532752373355576, 'rel_death_prob': 2.157371300339433}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:58,425] Trial 22 finished with value: 152.20222498556646 and parameters: {'beta': 0.01787126246282864, 'rel_death_prob': 1.4067405524477357}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:58,440] Trial 23 finished with value: 108.67655549140649 and parameters: {'beta': 0.016287080884003532, 'rel_death_prob': 1.4228314216285982}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:59,133] Trial 24 finished with value: 1043.578296398277 and parameters: {'beta': 0.04139525367112373, 'rel_death_prob': 1.8552136229241794}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:59,167] Trial 25 finished with value: 1072.8320824266111 and parameters: {'beta': 0.04331646738147564, 'rel_death_prob': 1.9784709995301006}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:59,850] Trial 26 finished with value: 1773.4016520850912 and parameters: {'beta': 0.06623330075609171, 'rel_death_prob': 2.3355578526362084}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:18:59,911] Trial 27 finished with value: 1176.4762179686459 and parameters: {'beta': 0.074159207981216, 'rel_death_prob': 1.1626891167030116}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:00,531] Trial 28 finished with value: 812.8126526624328 and parameters: {'beta': 0.030069461306962513, 'rel_death_prob': 1.5516598628264255}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:00,601] Trial 29 finished with value: 1029.609184171959 and parameters: {'beta': 0.03182370479877137, 'rel_death_prob': 1.537187909622062}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:01,236] Trial 30 finished with value: 786.6457565395035 and parameters: {'beta': 0.0533011915607324, 'rel_death_prob': 0.9695367261374306}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:01,322] Trial 31 finished with value: 732.0109250788294 and parameters: {'beta': 0.054091620812570594, 'rel_death_prob': 0.7907766737090607}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:01,739] Trial 32 finished with value: 98.82832970644402 and parameters: {'beta': 0.014832783830945748, 'rel_death_prob': 1.1920335054829494}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:01,837] Trial 33 finished with value: 97.22076653195363 and parameters: {'beta': 0.014859810424243853, 'rel_death_prob': 1.2907609077187872}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:02,276] Trial 34 finished with value: 78.65479415552693 and parameters: {'beta': 0.016028187686789437, 'rel_death_prob': 1.1906150772779627}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:02,436] Trial 35 finished with value: 163.32071323888619 and parameters: {'beta': 0.018926560810162946, 'rel_death_prob': 1.2049848104208796}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:03,003] Trial 36 finished with value: 852.7440378380779 and parameters: {'beta': 0.036960312899908004, 'rel_death_prob': 1.2029508909540283}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:03,147] Trial 37 finished with value: 563.7677088422082 and parameters: {'beta': 0.03548577322947463, 'rel_death_prob': 0.8209335304001841}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:03,746] Trial 38 finished with value: 699.9695785406582 and parameters: {'beta': 0.07427079125338718, 'rel_death_prob': 0.7649828793514049}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:03,891] Trial 39 finished with value: 750.6797086645646 and parameters: {'beta': 0.07767146464558078, 'rel_death_prob': 0.6758839509079665}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:04,502] Trial 40 finished with value: 1160.0997024470398 and parameters: {'beta': 0.11286188643738713, 'rel_death_prob': 1.2816649953087922}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:04,563] Trial 41 finished with value: 299.25212061997604 and parameters: {'beta': 0.02088914265292178, 'rel_death_prob': 1.0697040310123116}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:04,951] Trial 42 finished with value: 146.63343251765332 and parameters: {'beta': 0.0055422515559087355, 'rel_death_prob': 1.0445670024137963}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:05,028] Trial 43 finished with value: 141.3400985921748 and parameters: {'beta': 0.005153630810056105, 'rel_death_prob': 1.5480838356530873}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:05,535] Trial 44 finished with value: 101.56181995825375 and parameters: {'beta': 0.01620146924661596, 'rel_death_prob': 1.540241783275919}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:05,581] Trial 45 finished with value: 86.13125638406538 and parameters: {'beta': 0.014938033027223081, 'rel_death_prob': 1.8470751795099352}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:06,213] Trial 46 finished with value: 949.2825420793179 and parameters: {'beta': 0.02656055471651368, 'rel_death_prob': 2.575925862763545}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:06,274] Trial 47 finished with value: 551.0047963760715 and parameters: {'beta': 0.024137563660001755, 'rel_death_prob': 1.288385699135993}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:07,016] Trial 48 finished with value: 2406.8424967802102 and parameters: {'beta': 0.17322037104300111, 'rel_death_prob': 1.781779542423911}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:07,079] Trial 49 finished with value: 2089.445419016743 and parameters: {'beta': 0.1562924734000758, 'rel_death_prob': 1.7960281542311736}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:07,737] Trial 50 finished with value: 1350.2752364879868 and parameters: {'beta': 0.05036522103215835, 'rel_death_prob': 1.994624604900547}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:07,815] Trial 51 finished with value: 1427.846515965715 and parameters: {'beta': 0.06263961499078519, 'rel_death_prob': 1.9808191438580094}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:08,248] Trial 52 finished with value: 90.38259981347426 and parameters: {'beta': 0.014086698697712254, 'rel_death_prob': 2.0654919637269904}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:08,351] Trial 53 finished with value: 77.7745703246436 and parameters: {'beta': 0.01414528610083618, 'rel_death_prob': 2.1486985103526512}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:08,763] Trial 54 finished with value: 83.13196695829816 and parameters: {'beta': 0.012775279321798352, 'rel_death_prob': 2.3858273590372354}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:08,872] Trial 55 finished with value: 78.00850468534884 and parameters: {'beta': 0.012840998151474266, 'rel_death_prob': 2.3155549604099854}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:09,454] Trial 56 finished with value: 1207.897144379802 and parameters: {'beta': 0.036007444936156194, 'rel_death_prob': 2.333253274872288}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:09,563] Trial 57 finished with value: 1161.803859306302 and parameters: {'beta': 0.03326851556121878, 'rel_death_prob': 2.3478518010335714}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:10,122] Trial 58 finished with value: 837.0747657325576 and parameters: {'beta': 0.024987544737479182, 'rel_death_prob': 2.6123294000345783}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:10,254] Trial 59 finished with value: 853.296065195186 and parameters: {'beta': 0.02512906087726851, 'rel_death_prob': 2.6387566212051285}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:10,616] Trial 60 finished with value: 121.36063862859173 and parameters: {'beta': 0.01017231764766837, 'rel_death_prob': 2.1464972579703137}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:10,774] Trial 61 finished with value: 119.70666607452146 and parameters: {'beta': 0.010481517664025261, 'rel_death_prob': 2.2312412676014235}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:11,130] Trial 62 finished with value: 121.65230714571211 and parameters: {'beta': 0.011015501825001123, 'rel_death_prob': 2.262399728443284}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:11,427] Trial 63 finished with value: 452.8596171781321 and parameters: {'beta': 0.02021484993497818, 'rel_death_prob': 2.4608664060544694}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:11,851] Trial 64 finished with value: 1472.7569169960475 and parameters: {'beta': 0.04660741518720626, 'rel_death_prob': 2.4636124691696106}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:12,163] Trial 65 finished with value: 1177.315472753919 and parameters: {'beta': 0.043746040004068, 'rel_death_prob': 2.1059832903043976}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:12,320] Trial 66 finished with value: 146.65896877914463 and parameters: {'beta': 0.005366636967938522, 'rel_death_prob': 2.0856206381248805}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:12,627] Trial 67 finished with value: 141.3400985921748 and parameters: {'beta': 0.0052590172187717485, 'rel_death_prob': 2.031911568972174}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:13,172] Trial 68 finished with value: 2411.990718124084 and parameters: {'beta': 0.1972252692257751, 'rel_death_prob': 1.8780552447071603}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:13,421] Trial 69 finished with value: 1972.8988097881602 and parameters: {'beta': 0.13059985773879623, 'rel_death_prob': 1.8996616094903087}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:13,704] Trial 70 finished with value: 71.16223297952658 and parameters: {'beta': 0.013439808949511656, 'rel_death_prob': 1.8706183387969688}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:14,130] Trial 71 finished with value: 1184.9460407691968 and parameters: {'beta': 0.030098375379112367, 'rel_death_prob': 2.746508059900468}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:14,219] Trial 72 finished with value: 116.55660167873164 and parameters: {'beta': 0.012210680470183047, 'rel_death_prob': 1.7095959089779877}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:14,670] Trial 73 finished with value: 68.24088466491985 and parameters: {'beta': 0.013968031506610806, 'rel_death_prob': 1.7134794848428805}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:14,854] Trial 74 finished with value: 310.4609850335302 and parameters: {'beta': 0.019794447863668557, 'rel_death_prob': 2.2168761627521487}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:15,341] Trial 75 finished with value: 488.8084558333703 and parameters: {'beta': 0.02302403582990528, 'rel_death_prob': 1.467694990878043}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:15,560] Trial 76 finished with value: 1143.4588311053872 and parameters: {'beta': 0.03989383594575377, 'rel_death_prob': 1.6008195127703608}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:16,069] Trial 77 finished with value: 1138.3203801572145 and parameters: {'beta': 0.040762291684869584, 'rel_death_prob': 1.6480858355267614}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:16,320] Trial 78 finished with value: 2062.616578585069 and parameters: {'beta': 0.10354999328193101, 'rel_death_prob': 2.3771871584571693}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:16,699] Trial 79 finished with value: 271.5858018386108 and parameters: {'beta': 0.01860825912540017, 'rel_death_prob': 1.912429734754961}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:17,043] Trial 80 finished with value: 861.9172181018786 and parameters: {'beta': 0.028933408788635845, 'rel_death_prob': 1.729931688131641}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:17,432] Trial 81 finished with value: 856.9637385086824 and parameters: {'beta': 0.03000482577695223, 'rel_death_prob': 1.7524694694002763}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:17,645] Trial 82 finished with value: 91.78920371275036 and parameters: {'beta': 0.01606351330171371, 'rel_death_prob': 2.2811369262199985}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:17,957] Trial 83 finished with value: 88.33448061464671 and parameters: {'beta': 0.014138021432871033, 'rel_death_prob': 1.8120653308408465}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:18,181] Trial 84 finished with value: 79.57165697028913 and parameters: {'beta': 0.012686928255514731, 'rel_death_prob': 2.1630863847941764}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:18,473] Trial 85 finished with value: 117.88071235066838 and parameters: {'beta': 0.011164452718083934, 'rel_death_prob': 1.9305483946438287}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:18,689] Trial 86 finished with value: 130.79295643291735 and parameters: {'beta': 0.009841540336732162, 'rel_death_prob': 2.1896364366524654}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:19,131] Trial 87 finished with value: 551.9505262690411 and parameters: {'beta': 0.021736243046118153, 'rel_death_prob': 2.414656711566095}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:19,364] Trial 88 finished with value: 698.2133499133988 and parameters: {'beta': 0.022537975017538826, 'rel_death_prob': 2.116458080311285}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:19,841] Trial 89 finished with value: 819.65648176933 and parameters: {'beta': 0.03529850099872517, 'rel_death_prob': 1.3390854772761518}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:20,066] Trial 90 finished with value: 753.183816671848 and parameters: {'beta': 0.03346997583493105, 'rel_death_prob': 1.353885517761058}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:20,455] Trial 91 finished with value: 139.9865657059111 and parameters: {'beta': 0.01777075287521817, 'rel_death_prob': 1.4734214929400045}. Best is trial 13 with value: 58.59128658347027.
[I 2026-02-19 04:19:20,616] Trial 92 finished with value: 52.71061864369143 and parameters: {'beta': 0.01517185719328714, 'rel_death_prob': 1.8030713111992847}. Best is trial 92 with value: 52.71061864369143.
[I 2026-02-19 04:19:20,997] Trial 93 finished with value: 52.26639872096638 and parameters: {'beta': 0.015563426866118045, 'rel_death_prob': 1.8138516716846957}. Best is trial 93 with value: 52.26639872096638.
[I 2026-02-19 04:19:21,109] Trial 94 finished with value: 139.53279744193276 and parameters: {'beta': 0.008789248390738583, 'rel_death_prob': 1.1297654600686484}. Best is trial 93 with value: 52.26639872096638.
[I 2026-02-19 04:19:21,507] Trial 95 finished with value: 137.56483989874317 and parameters: {'beta': 0.009764361030501593, 'rel_death_prob': 0.9032064253193886}. Best is trial 93 with value: 52.26639872096638.
[I 2026-02-19 04:19:21,798] Trial 96 finished with value: 532.4358262646001 and parameters: {'beta': 0.025379481230583922, 'rel_death_prob': 0.9202467589539084}. Best is trial 93 with value: 52.26639872096638.
[I 2026-02-19 04:19:22,197] Trial 97 finished with value: 897.6811964293645 and parameters: {'beta': 0.025741447483191657, 'rel_death_prob': 2.512035321314018}. Best is trial 93 with value: 52.26639872096638.
[I 2026-02-19 04:19:22,425] Trial 98 finished with value: 238.72007816316562 and parameters: {'beta': 0.018224568374285977, 'rel_death_prob': 2.5290375434955417}. Best is trial 93 with value: 52.26639872096638.
[I 2026-02-19 04:19:22,693] Trial 99 finished with value: 200.48374561442466 and parameters: {'beta': 0.018160861215862856, 'rel_death_prob': 2.293625394807339}. Best is trial 93 with value: 52.26639872096638.

Making results structure...
Processed 100 trials; 0 failed
Deleted study covasim_calibration in sqlite:///covasim_calibration.db
Removed existing calibration covasim_calibration.db
Calibration for 100 total trials completed in 33.6 s.

Initial parameter values:
#0. 'beta':           0.015
#1. 'rel_death_prob': 1.0

Best parameter values:
#0. 'beta':           0.015563426866118045
#1. 'rel_death_prob': 1.8138516716846957

Mismatch before calibration: 101.465
Mismatch after calibration:  52.2664
Percent improvement:         48.5%

So it improved the fit (see above), but let’s visualize this as a plot:

[6]:

# Plot the results
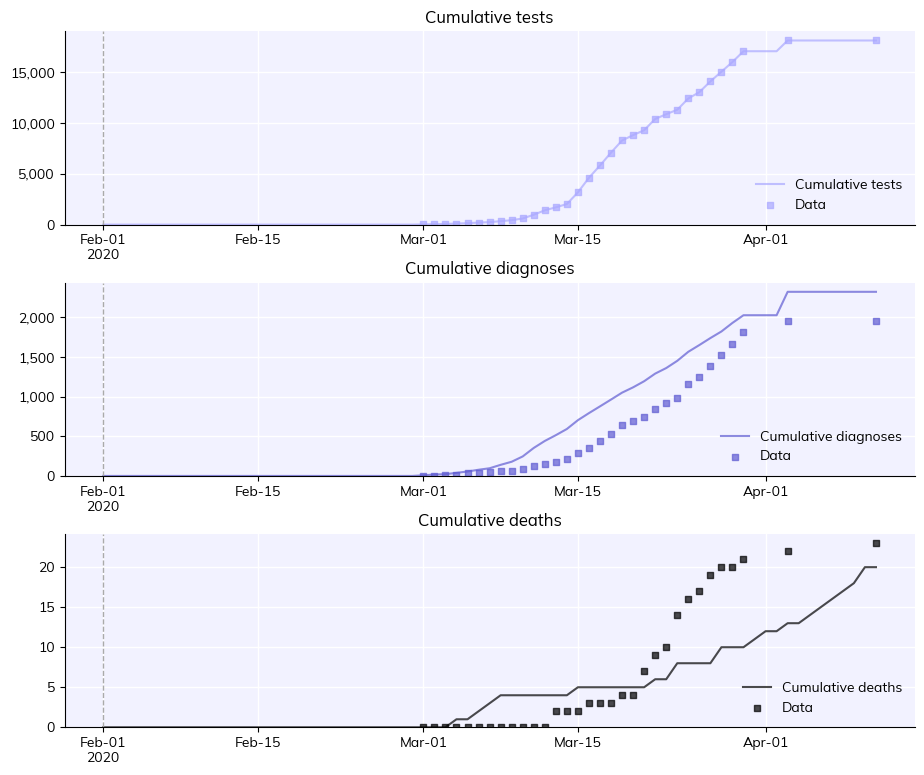
calib.plot_trend()
calib.plot_sims(to_plot=['cum_tests', 'cum_diagnoses', 'cum_deaths'])

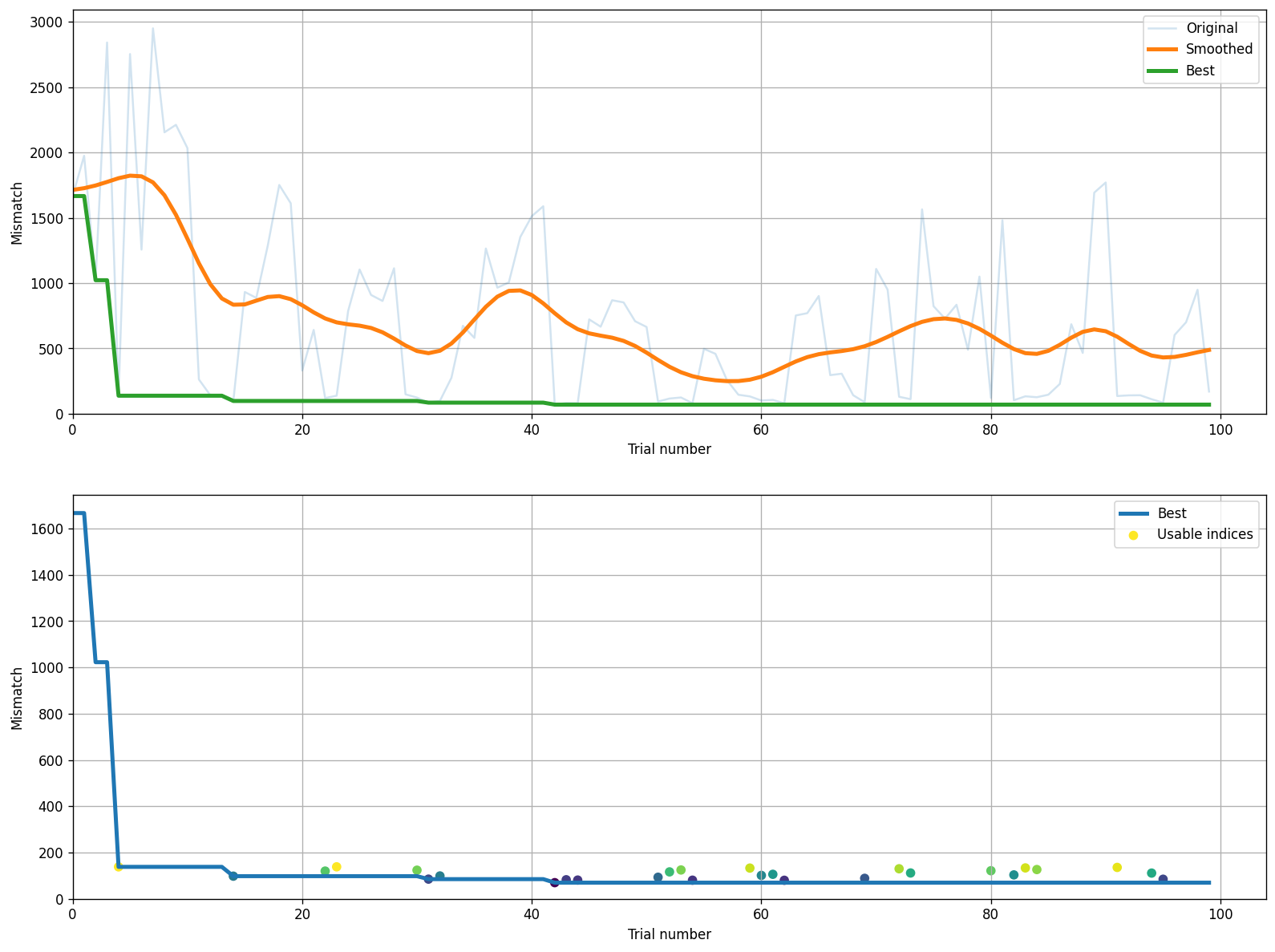
../_images/tutorials_tut_calibration_16_0.png

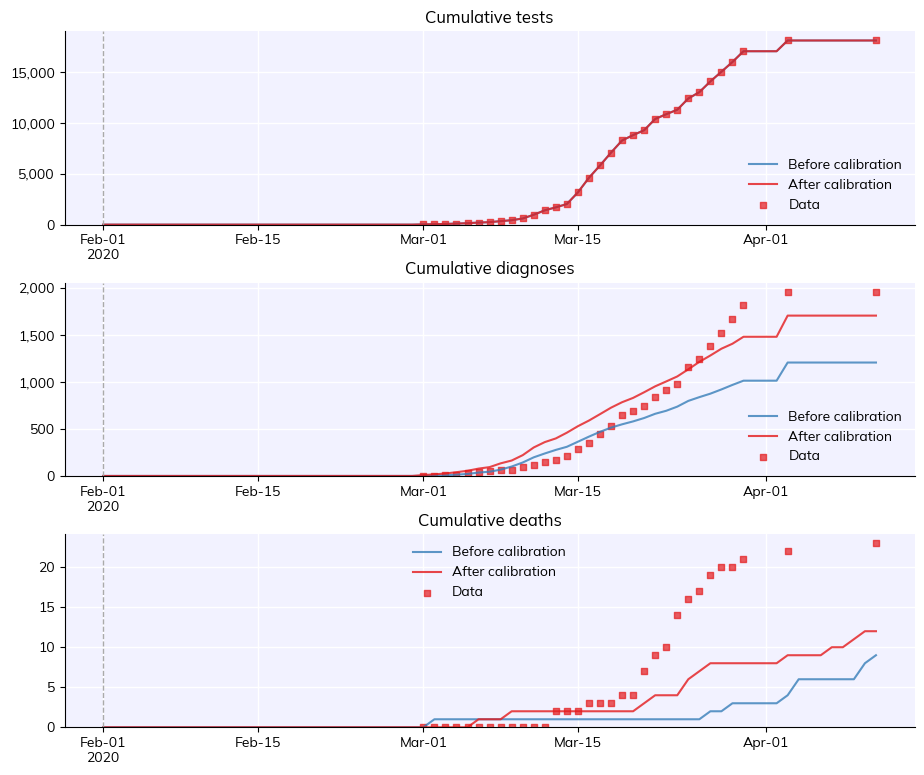
../_images/tutorials_tut_calibration_16_1.png

Compared to scipy.optimize.minimize(), Optuna took less time and produced a better fit. Specifically, the mismatch obtained with Optuna is almost half the smallest mismatch achieved with scipy.optimize. However, Optuna’s results are still far from perfect – running calibration runs, or more iterations, and calibrating more parameters beyond just these two, would still be required before the model could be considered “calibrated”.

Sometimes you want to calibrate a parameter that isn’t a built-in parameter – for example, part of an intervention. You can do this using the custom_fn keyword argument. In this example, we calibrate the test probability by modifying the test_prob intervention directly.

[7]:

pars = dict(
    verbose = 0,
    start_day = '2020-02-05',
    pop_size = 1000,
    pop_scale = 4,
    interventions = cv.test_prob(symp_prob=0.01),
)

sim = cv.Sim(pars, datafile='example_data.csv')

calib_pars = dict(
    beta      = [0.013, 0.005, 0.020],
    test_prob = [0.01, 0.00, 0.30]
)

def set_test_prob(sim, calib_pars):
    tp = sim.get_intervention(cv.test_prob)
    tp.symp_prob = calib_pars['test_prob']
    return sim

calib = sim.calibrate(calib_pars=calib_pars, custom_fn=set_test_prob, total_trials=60)
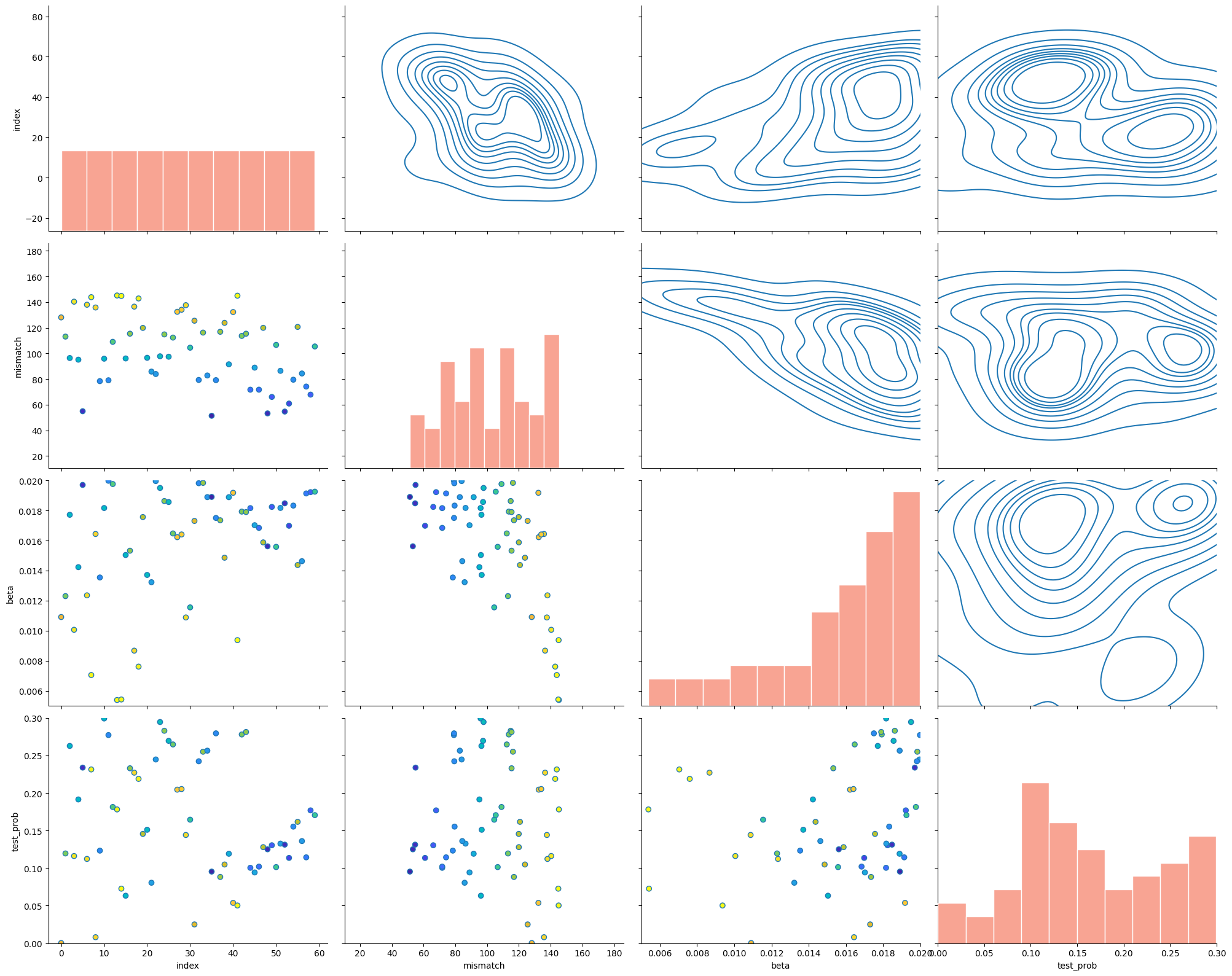
calib.plot_all()
calib.plot_sims(to_plot=['cum_deaths', 'cum_diagnoses'])

Could not delete study, skipping...
'Record does not exist.'
Removed existing calibration covasim_calibration.db

[I 2026-02-19 04:19:24,993] A new study created in RDB with name: covasim_calibration
[I 2026-02-19 04:19:25,368] Trial 0 finished with value: 137.95831427268368 and parameters: {'beta': 0.011287728355263212, 'test_prob': 0.022152832537377543}. Best is trial 0 with value: 137.95831427268368.
[I 2026-02-19 04:19:25,402] Trial 1 finished with value: 142.1164404257931 and parameters: {'beta': 0.009139015110050795, 'test_prob': 0.09011235359013371}. Best is trial 0 with value: 137.95831427268368.
[I 2026-02-19 04:19:25,586] Trial 2 finished with value: 74.64300712515626 and parameters: {'beta': 0.014778135036873915, 'test_prob': 0.2285140078466695}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:25,652] Trial 3 finished with value: 79.13580170935583 and parameters: {'beta': 0.014572261304204304, 'test_prob': 0.07209429510464013}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:25,782] Trial 4 finished with value: 145.50341649102532 and parameters: {'beta': 0.00727563038887824, 'test_prob': 0.04765581249921812}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:25,842] Trial 5 finished with value: 136.9093180119895 and parameters: {'beta': 0.007756876130001679, 'test_prob': 0.1987673609032411}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:25,993] Trial 6 finished with value: 85.67239343473479 and parameters: {'beta': 0.017441300862094958, 'test_prob': 0.262615774666134}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,031] Trial 7 finished with value: 145.49857924093175 and parameters: {'beta': 0.006839022877589452, 'test_prob': 0.11028245736100163}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,209] Trial 8 finished with value: 94.04674277093184 and parameters: {'beta': 0.017425852998090182, 'test_prob': 0.25001833520030625}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,265] Trial 9 finished with value: 141.99594594872153 and parameters: {'beta': 0.010038901588730668, 'test_prob': 0.28955696415554516}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,402] Trial 10 finished with value: 146.07020523662626 and parameters: {'beta': 0.010799811577732188, 'test_prob': 0.01174505072293156}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,483] Trial 11 finished with value: 110.92888047682331 and parameters: {'beta': 0.01383114115662891, 'test_prob': 0.18595827684396868}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,609] Trial 12 finished with value: 133.33629594399562 and parameters: {'beta': 0.0143509120930382, 'test_prob': 0.17588885998617734}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,694] Trial 13 finished with value: 127.50726773426156 and parameters: {'beta': 0.014456669651461373, 'test_prob': 0.13547170875651277}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,822] Trial 14 finished with value: 84.3538193236833 and parameters: {'beta': 0.015235359961636078, 'test_prob': 0.1272802492132599}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:26,905] Trial 15 finished with value: 123.89304737004028 and parameters: {'beta': 0.019296276278857383, 'test_prob': 0.07528509014702765}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,036] Trial 16 finished with value: 127.11438313249059 and parameters: {'beta': 0.01960999823138188, 'test_prob': 0.08080498786859906}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,098] Trial 17 finished with value: 143.76197703105237 and parameters: {'beta': 0.012686460342182387, 'test_prob': 0.24616897213913458}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,240] Trial 18 finished with value: 110.38331185821406 and parameters: {'beta': 0.012303524741866415, 'test_prob': 0.15604174405570276}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,301] Trial 19 finished with value: 144.26399140255728 and parameters: {'beta': 0.005034907248551823, 'test_prob': 0.2233057465382483}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,442] Trial 20 finished with value: 130.5892320156799 and parameters: {'beta': 0.01606362071803354, 'test_prob': 0.22160012101839305}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,520] Trial 21 finished with value: 112.98023059072327 and parameters: {'beta': 0.016852841521668695, 'test_prob': 0.045764948974066064}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,656] Trial 22 finished with value: 80.97623418673359 and parameters: {'beta': 0.01615257751441868, 'test_prob': 0.12838132725851206}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,738] Trial 23 finished with value: 98.43661945802856 and parameters: {'beta': 0.015552040650759744, 'test_prob': 0.11628344522943809}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,870] Trial 24 finished with value: 123.68324289458643 and parameters: {'beta': 0.012718415204631704, 'test_prob': 0.1552507898395915}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:27,951] Trial 25 finished with value: 128.26763996769301 and parameters: {'beta': 0.01302756556810615, 'test_prob': 0.14388479657253894}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,089] Trial 26 finished with value: 81.61714014389078 and parameters: {'beta': 0.018290795193971122, 'test_prob': 0.05472247348628574}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,176] Trial 27 finished with value: 81.42930861889015 and parameters: {'beta': 0.018285888123021198, 'test_prob': 0.054866443464184136}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,307] Trial 28 finished with value: 118.38958183453674 and parameters: {'beta': 0.016410998984538787, 'test_prob': 0.10634500175748257}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,397] Trial 29 finished with value: 77.21245606258167 and parameters: {'beta': 0.016427289097978085, 'test_prob': 0.09449067363460939}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,520] Trial 30 finished with value: 79.27584366053597 and parameters: {'beta': 0.01512776655841665, 'test_prob': 0.2998774230017429}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,596] Trial 31 finished with value: 118.19975993604933 and parameters: {'beta': 0.011619846648291174, 'test_prob': 0.09836243168310342}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,738] Trial 32 finished with value: 104.10097612319214 and parameters: {'beta': 0.014878259306219737, 'test_prob': 0.29897001700118686}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,809] Trial 33 finished with value: 124.69698500445114 and parameters: {'beta': 0.01470893280747204, 'test_prob': 0.2950338597649225}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:28,953] Trial 34 finished with value: 120.96204472372678 and parameters: {'beta': 0.013606791579561447, 'test_prob': 0.28648137215089275}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:29,017] Trial 35 finished with value: 130.92101924367063 and parameters: {'beta': 0.013448629416136471, 'test_prob': 0.26456593214106294}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:29,162] Trial 36 finished with value: 127.55609169427956 and parameters: {'beta': 0.015503612123023189, 'test_prob': 0.2742842615804292}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:29,233] Trial 37 finished with value: 104.39391424316062 and parameters: {'beta': 0.017670089046550014, 'test_prob': 0.02684801931655989}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:29,375] Trial 38 finished with value: 92.40443060939619 and parameters: {'beta': 0.017305554776719693, 'test_prob': 0.22044567454812988}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:29,445] Trial 39 finished with value: 101.58773789040909 and parameters: {'beta': 0.017003786788984076, 'test_prob': 0.21078200564399402}. Best is trial 2 with value: 74.64300712515626.
[I 2026-02-19 04:19:29,593] Trial 40 finished with value: 62.40789384382734 and parameters: {'beta': 0.01866597690688154, 'test_prob': 0.06746842603969389}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:29,663] Trial 41 finished with value: 133.92534570799944 and parameters: {'beta': 0.011461416453506689, 'test_prob': 0.07482003221111352}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:29,810] Trial 42 finished with value: 67.38632242351542 and parameters: {'beta': 0.018687838931861486, 'test_prob': 0.07122723125680046}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:29,884] Trial 43 finished with value: 124.65370959691401 and parameters: {'beta': 0.018257053804439323, 'test_prob': 0.034385899815484955}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,027] Trial 44 finished with value: 98.38300413112466 and parameters: {'beta': 0.0188895715155071, 'test_prob': 0.03010149444198188}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,107] Trial 45 finished with value: 107.87622028847869 and parameters: {'beta': 0.01890226084988238, 'test_prob': 0.01087212700773571}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,243] Trial 46 finished with value: 79.20932890727602 and parameters: {'beta': 0.019649194610491992, 'test_prob': 0.06541965706735817}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,318] Trial 47 finished with value: 101.97036586761428 and parameters: {'beta': 0.017784504947848483, 'test_prob': 0.08884028699095217}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,461] Trial 48 finished with value: 99.56781930498605 and parameters: {'beta': 0.01787673992225281, 'test_prob': 0.08691520372169798}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,524] Trial 49 finished with value: 138.71643803355636 and parameters: {'beta': 0.009124936596249182, 'test_prob': 0.09790639251108332}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,668] Trial 50 finished with value: 113.90851432134106 and parameters: {'beta': 0.016517647892655037, 'test_prob': 0.17056133849884925}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,739] Trial 51 finished with value: 78.61800815604204 and parameters: {'beta': 0.01994471852824694, 'test_prob': 0.17631937796868613}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,882] Trial 52 finished with value: 114.49138306870303 and parameters: {'beta': 0.019778800551770635, 'test_prob': 0.06915986652848959}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:30,953] Trial 53 finished with value: 125.47256921615757 and parameters: {'beta': 0.019883748984103396, 'test_prob': 0.06546018234395144}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:31,093] Trial 54 finished with value: 114.83328866034975 and parameters: {'beta': 0.018913730130438417, 'test_prob': 0.1894942649337773}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:31,172] Trial 55 finished with value: 90.02656560609685 and parameters: {'beta': 0.014150205477259264, 'test_prob': 0.2387033143084322}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:31,303] Trial 56 finished with value: 117.64815647986023 and parameters: {'beta': 0.014180973142043352, 'test_prob': 0.24243549514594598}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:31,393] Trial 57 finished with value: 98.14857992784935 and parameters: {'beta': 0.01906212085417837, 'test_prob': 0.11892746577682864}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:31,515] Trial 58 finished with value: 83.05959623754926 and parameters: {'beta': 0.015819121555089966, 'test_prob': 0.12065442759112249}. Best is trial 40 with value: 62.40789384382734.
[I 2026-02-19 04:19:31,583] Trial 59 finished with value: 123.37719528201868 and parameters: {'beta': 0.015877088554579664, 'test_prob': 0.0015225605944623466}. Best is trial 40 with value: 62.40789384382734.

Making results structure...
Processed 60 trials; 0 failed
Deleted study covasim_calibration in sqlite:///covasim_calibration.db
Removed existing calibration covasim_calibration.db
Calibration for 60 total trials completed in 7.1 s.

Initial parameter values:
#0. 'beta':      0.013
#1. 'test_prob': 0.01

Best parameter values:
#0. 'beta':      0.01866597690688154
#1. 'test_prob': 0.06746842603969389

Mismatch before calibration: 141.953
Mismatch after calibration:  62.4079
Percent improvement:         56.0%

../_images/tutorials_tut_calibration_18_3.png

../_images/tutorials_tut_calibration_18_4.png